
分析 设所求圆的方程为圆C:(x-a)2+(y-b)2=r2,由圆C与直线y=0相切,且半径为4,则圆心C的坐标为C1(a,4)或C2(a,-4),又已知两圆相切,求出|CA|=7或|CA|=1,然后分类即可求出求出圆的方程.
解答 解:由题意,设所求圆的方程为圆C:(x-a)2+(y-b)2=r2.
圆C与直线y=0相切,且半径为4,则圆心C的坐标为C1(a,4)或C2(a,-4).
又已知圆x2+y2-4x-2y-4=0即(x-2)2+(y-1)2=9的圆心A的坐标为(2,1),半径为3,
若两圆相切,则|CA|=4+3=7或|CA|=4-3=1.
①当C1(a,4)时,有(a-2)2+(4-1)2=72或(a-2)2+(4-1)2=12(无解),故可得a=2±2$\sqrt{10}$.
∴所求圆方程为(x-2-2$\sqrt{10}$)2+(y-4)2=42或(x-2+2$\sqrt{10}$)2+(y-4)2=42.
②当C2(a,-4)时,(a-2)2+(-4-1)2=72或(a-2)2+(-4-1)2=12(无解),故a=2±2$\sqrt{6}$.
∴所求圆的方程为(x-2-2$\sqrt{6}$)2+(y+4)2=42或(x-2+2$\sqrt{6}$)2+(y+4)2=16.
故答案为:(x-2-2$\sqrt{10}$)2+(y-4)2=16或(x-2+2$\sqrt{10}$)2+(y-4)2=16或(x-2-2$\sqrt{6}$)2+(y+4)2=16或(x-2+2$\sqrt{6}$)2+(y+4)2=16.
点评 本题考查圆的方程,考查待定系数法,考查学生的计算能力,属于中档题.


 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案科目:高中数学 来源: 题型:选择题
| A. | 已知实数a,b,则“a>b”是“a2>b2”的必要不充分条件 | |
| B. | “存在x0∈R,使得$x_0^2-1<0$”的否定是“对任意x∈R,均有x2-1>0” | |
| C. | 函数$f(x)={x^{\frac{1}{3}}}-{(\frac{1}{2})^x}$的零点在区间$(\frac{1}{3},\frac{1}{2})$内 | |
| D. | 设m,n是两条直线,α,β是空间中两个平面,若m?α,n?β,m⊥n,则α⊥β |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
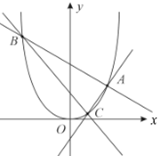 如图,过顶点在原点O,对称轴为y轴的抛物线E上的定点A(2,1)作斜率分别为k1,k2的直线,分别交抛物线E于B,C两点.
如图,过顶点在原点O,对称轴为y轴的抛物线E上的定点A(2,1)作斜率分别为k1,k2的直线,分别交抛物线E于B,C两点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2014 | B. | 2015 | C. | -2015 | D. | -2016 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | p∧q | B. | ¬p∧q | C. | p∧¬q | D. | ¬p∧¬q |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
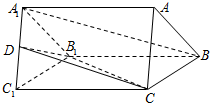 如图,在三棱柱ABC-A1B1C1中,△ABC是等边三角形,BC=CC1=4,D是A1C1中点.
如图,在三棱柱ABC-A1B1C1中,△ABC是等边三角形,BC=CC1=4,D是A1C1中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com