
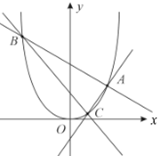
 如图,过顶点在原点O,对称轴为y轴的抛物线E上的定点A(2,1)作斜率分别为k1,k2的直线,分别交抛物线E于B,C两点.
如图,过顶点在原点O,对称轴为y轴的抛物线E上的定点A(2,1)作斜率分别为k1,k2的直线,分别交抛物线E于B,C两点.分析 (1)抛物线E的方程为x2=2py,把点A的坐标(2,1)代入x2=2py得p=2,即可求抛物线E的标准方程和准线方程;
(2)设直线BC的方程为y=kx+m,与抛物线方程联立,利用k1+k2=k1k2,结合韦达定理,利用△ABC的面积为8$\sqrt{5}$,求直线BC的方程.
解答 解:(1)抛物线E的方程为x2=2py,把点A的坐标(2,1)代入x2=2py得p=2,
∴抛物线E的方程为x2=4y,其准线方程为y=-1.
(2)∵B,C两点在抛物线E上,∴直线BC的斜率存在,
设直线BC的方程为y=kx+m,B(x1,y1),C(x2,y2)
由$\left\{\begin{array}{l}y=kx+m\\{x^2}=4y\end{array}\right.$⇒x2-4kx-4m=0,∴x1+x2=4k,x1x2=-4m,△=16k2+16m>0,∴k2+m>0
∵${y_1}=\frac{x_1^2}{4}$,${y_2}=\frac{x_2^2}{4}$,∴${k_1}=\frac{{{y_1}-1}}{{{x_1}-2}}=\frac{{\frac{1}{4}x_1^2-1}}{{{x_1}-2}}=\frac{{{x_1}+2}}{4}$,
同理,${k_2}=\frac{{{x_2}+2}}{4}$.
由k1+k2=k1k2,得$\frac{{{x_1}+2}}{4}+\frac{{{x_2}+2}}{4}=\frac{{({x_1}+2)({x_2}+2)}}{16}$
∴2(x1+x2)-x1x2+12=0,∴8k+4m+12=0,∴2k+m+3=0,∴m=-2k-3,
由△>0得k>3或k<-1.
又$|BC|=\sqrt{1+{k^2}}|{x_1}-{x_2}|=\sqrt{1+{k^2}}•4\sqrt{{k^2}+m}$,
点A(2,1)到直线BC的距离$d=\frac{|2k-1+m|}{{\sqrt{{k^2}+1}}}$.
${S_{△ABC}}=\frac{1}{2}|BC|d=2\sqrt{{k^2}+m}|2k-1+m|=8\sqrt{5}$,
又m=-2k-3,∴k2-2k-8=0,解得k=4或k=-2,都满足△>0.
当k=4时,m=-2×4-3=-11,则直线BC的方程为:y=4x-11;
当k=-2时,m=(-2)×(-2)-3=1,则直线BC的方程为:y=-2x+1.
点评 本题主要考查了抛物线的方程与几何性质,考查直线与抛物线的位置关系的应用,直线与曲线联立,根据方程的根与系数的关系代入运算,这是处理这类问题的最为常用的方法.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
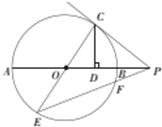 如图,点C为圆O上一点,CP为圆的切线,CE为圆的直径,CP=3.
如图,点C为圆O上一点,CP为圆的切线,CE为圆的直径,CP=3.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [7,8] | B. | [0,8] | C. | [$\frac{11}{2}$,8] | D. | [$\frac{11}{2}$,7] |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com