
【题目】在△ABC中,角A,B,C的对边分别为a,b,c,且cosC= ![]() .
.
(1)求B;
(2)设CM是角C的平分线,且CM=1,b=6,求cos∠BCM.
 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案科目:高中数学 来源: 题型:
【题目】为了节约用水,学校改革澡堂收费制度,实行计时收费,洗澡时间在30分钟以内(含30分钟),每分钟收费0.1元,30分钟以上超出的部分每分钟0.2元,请设计程序,使用基本语句完成澡堂计费工作,要求输入时间,输出费用.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设 ![]() ,
, ![]() ,
, ![]() 均为非零向量,已知命题p:
均为非零向量,已知命题p: ![]() =
= ![]() 是
是 ![]()
![]() =
= ![]()
![]() 的必要不充分条件,命题q:x>1是|x|>1成立的充分不必要条件,则下列命题是真命题的是( )
的必要不充分条件,命题q:x>1是|x|>1成立的充分不必要条件,则下列命题是真命题的是( )
A.p∧q
B.p∨q
C.(¬p)∧(¬q)
D.p∨(¬q)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知常数![]() 数列
数列![]() 的前
的前![]() 项和为
项和为![]() ,
,![]() 且
且![]()
(1)求数列![]() 的通项公式;
的通项公式;
(2)若![]() 且数列
且数列![]() 是单调递增数列,求实数
是单调递增数列,求实数![]() 的取值范围;
的取值范围;
(3)若![]() 数列
数列![]() 满足:
满足:![]() 对于任意给定的正整数
对于任意给定的正整数![]() ,是否存在
,是否存在![]() 使
使![]() ?若存在,求
?若存在,求![]() 的值(只要写出一组即可);若不存在,说明理由.
的值(只要写出一组即可);若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在某小学体育素质达标运动会上,对10名男生和10名女生在一分钟跳绳的次数进行统计,得到如下所示茎叶图: 
(1)已知男生组中数据的中位数为125,女生组数据的平均数为124,求x,y的值;
(2)现从这20名学生中任意抽取一名男生和一名女生对他们进行训练,记一分钟内跳绳次数不低于115且不超过125的学生被选上的人数为X,求X的分布列和数学期望E(X).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知平面内动点P与点A(﹣3,0)和点B(3,0)的连线的斜率之积为﹣ ![]() .
.
(1)求动点P的轨迹方程;
(2)设点P的轨迹且曲线C,过点(1,0)的直线与曲线C交于M,N两点,记△AMB的面积为S1 , △ANB的面积为S2 , 当S1﹣S2取得最大值时,求 ![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】三棱锥P﹣ABC中,底面△ABC满足BA=BC, ![]() ,P在面ABC的射影为AC的中点,且该三棱锥的体积为
,P在面ABC的射影为AC的中点,且该三棱锥的体积为 ![]() ,当其外接球的表面积最小时,P到面ABC的距离为( )
,当其外接球的表面积最小时,P到面ABC的距离为( )
A.2
B.3
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直三棱柱![]() 中,∠BAC=90°,AB=AC=AA1=2,E是BC中点.
中,∠BAC=90°,AB=AC=AA1=2,E是BC中点.
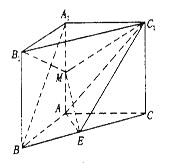
(Ⅰ)求证:A1B//平面AEC1;
(Ⅱ)在棱AA1上存在一点M,满足![]() ,求平面MEC1与平面ABB1A1所成锐二面角的余弦值。
,求平面MEC1与平面ABB1A1所成锐二面角的余弦值。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com