
分析 (1)直线y=-3x+b与二次函数y=-x2+2x-1联立可得x2-5x+b+1=0,利用弦长公式,建立方程,即可求b的值;
(2)利用中点坐标公式,求Q点的轨迹方程;
(3)表示出|$\overrightarrow{OQ}$|,利用b∈[-3,-$\frac{3}{4}$),求|$\overrightarrow{OQ}$|的取值范围.
解答 解:(1)直线y=-3x+b与二次函数y=-x2+2x-1联立可得x2-5x+b+1=0,
设A(x1,y1),B(x2,y2),则x1+x2=5,x1x2=b+1,△>0,可得b<$\frac{21}{4}$.
∵|AB|=3,
∴$\sqrt{1+9}$•$\sqrt{25-4b-4}$=3,
∴b=$\frac{201}{40}$;
(2)设Q(x,y),则x=2.5,y=-7.5+b,
∴Q点的轨迹方程是x=2.5(y<-$\frac{9}{4}$);
(3)|$\overrightarrow{OQ}$|=$\sqrt{\frac{({x}_{1}+{x}_{2})^{2}}{4}+\frac{({y}_{1}+{y}_{2})^{2}}{4}}$=$\sqrt{\frac{25}{4}+\frac{(2b-15)^{2}}{4}}$,
∵b∈[-3,-$\frac{3}{4}$),
∴$\frac{\sqrt{1189}}{4}$≤|$\overrightarrow{OQ}$|≤$\frac{\sqrt{469}}{2}$.
点评 本题考查直线与二次函数的关系,考查轨迹方程,考查学生的计算能力,属于中档题.


科目:高中数学 来源: 题型:解答题
 已知A={x|x具有性质p},B={x|x具有性质q},c={x|x具有性质r},集台A,B,C之间的关系如图所示:(注:每-个集合均是一个圆及其内部)
已知A={x|x具有性质p},B={x|x具有性质q},c={x|x具有性质r},集台A,B,C之间的关系如图所示:(注:每-个集合均是一个圆及其内部)查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 存在某个位置,使得$\overrightarrow{AD}$•$\overrightarrow{BC}$=0 | |
| B. | 存在某个位置,使得$\overrightarrow{AB}$•$\overrightarrow{CD}$=0 | |
| C. | 存在某个位置,使得$\overrightarrow{AC}$•$\overrightarrow{BD}$=0 | |
| D. | 对任意位置,$\overrightarrow{AD}$•$\overrightarrow{BC}$,$\overrightarrow{AB}$•$\overrightarrow{CD}$,$\overrightarrow{AC}$•$\overrightarrow{BD}$均不等于零 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
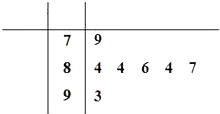 某校举行2010年元旦汇演,如图是7位评委为某选手打出的分数的茎叶统计图,去掉一个最高分和一个最低分后,所剩数据的平均数是85,方差为1.6.
某校举行2010年元旦汇演,如图是7位评委为某选手打出的分数的茎叶统计图,去掉一个最高分和一个最低分后,所剩数据的平均数是85,方差为1.6.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com