
已知 R,函数
R,函数 .(
.(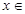 R,e为自然对数的底数)
R,e为自然对数的底数)
(Ⅰ)当 时,求函数
时,求函数 的单调递减区间;
的单调递减区间;
(Ⅱ)若函数 内单调递减,求a的取值范围;
内单调递减,求a的取值范围;
(Ⅲ)函数 是否为R上的单调函数,若是,求出a的取值范围;若不是,请说明理由.
是否为R上的单调函数,若是,求出a的取值范围;若不是,请说明理由.
(Ⅰ)当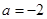 时,
时,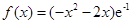
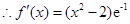 ……………………………………………………………………1分
……………………………………………………………………1分
令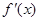
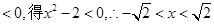 ……………………………………………2分
……………………………………………2分
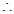
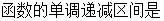 (-
(-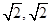 ).
).
(注:写成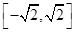 也对) ………………………………………………………3分
也对) ………………………………………………………3分
(Ⅱ)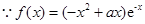
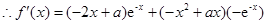
=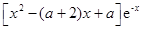 . ………………………………………………………………4分
. ………………………………………………………………4分
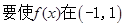 上单调递减,
上单调递减,
则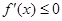 对
对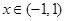 都成立,
都成立,
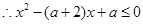 对
对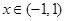 都成立.…………………………………………5分
都成立.…………………………………………5分
令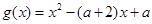 ,则
,则
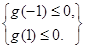 …………………………………………………………………………7分
…………………………………………………………………………7分
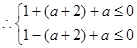
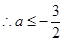 . (注:不带等号扣1分) ………………………………………………8分
. (注:不带等号扣1分) ………………………………………………8分
(Ⅲ)①若函数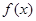 在R上单调递减,则
在R上单调递减,则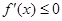 对
对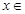 R 都成立
R 都成立
即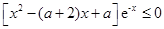 对
对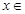 R都成立.…………………………………………9分
R都成立.…………………………………………9分
 对
对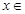 R都成立
R都成立
令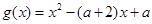 ,
,
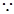 图象开口向上
图象开口向上 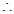 不可能对
不可能对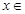 R都成立
R都成立
②若函数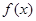 在R上单调递减,则
在R上单调递减,则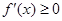 对
对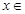 R 都成立,
R 都成立,
即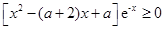 对
对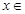 R都成立,
R都成立,
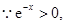
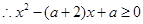 对
对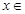 R都成立.
R都成立.
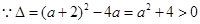
故函数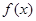 不可能在R上单调递增.
不可能在R上单调递增.
综上可知,函数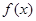 不可能是R上的单调函数
不可能是R上的单调函数
【解析】略


科目:高中数学 来源: 题型:
| 1 |
| 2 |
| (x-1)2 |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 | 2 |
查看答案和解析>>
科目:高中数学 来源:四川省成都市2011届高三第一次诊断性检测数学理科试题 题型:013
已知
R上的连续函数g(x)满足:①当x>0时,a≥1
或a≤00≤a≤1
-![]() -
-![]()
![]()
a∈R
查看答案和解析>>
科目:高中数学 来源:浙江省杭州市西湖高级中学2011-2012学年高三10月月考试题数学理 题型:解答题
本小题满分15分)已知 R,函数.(
R,函数.( R,e为自然对数的底数)
R,e为自然对数的底数)
(1)当a=-2时,求函数f(x)的单调递减区间;
(2)若函数f(x)在(-1,1)内单调递减,求a的取值范围;
(3)函数f(x)是否为R上的单调函数,若是,求出a的取值范围;若不是,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com