
分析 由题意可得f(x)=a(x-1)(x-2),求出导数,可得xn+1=$\frac{{{x}_{n}}^{2}-2}{2{x}_{n}-3}$,求得an+1=ln$\frac{{x}_{n+1}-2}{{x}_{n+1}-1}$=2ln$\frac{{x}_{n}-2}{{x}_{n}-1}$=2an,运用等比数列的通项公式即可得到所求.
解答 解:函数f(x)=ax2+bx+c(a>0)有两个零点1,2,
可得f(x)=a(x-1)(x-2),
f′(x)=a(2x-3),
则xn+1=xn-$\frac{f({x}_{n})}{f′({x}_{n})}$=xn-$\frac{a({x}_{n}-1)({x}_{n}-2)}{a(2{x}_{n}-3)}$=$\frac{{{x}_{n}}^{2}-2}{2{x}_{n}-3}$,
由a1=$\frac{1}{2}$,xn>2,
则an+1=ln$\frac{{x}_{n+1}-2}{{x}_{n+1}-1}$=ln$\frac{({x}_{n}-2)^{2}}{({x}_{n}-1)^{2}}$=2ln$\frac{{x}_{n}-2}{{x}_{n}-1}$=2an,
即有an=a1qn-1=$\frac{1}{2}$•2n-1=2n-2.
故答案为:2n-2(n∈N*).
点评 本题考查数列的通项公式的求法,注意运用化简变形,以及等比数列的定义和通项公式,考查二次函数的解析式的求法和零点的定义,考查运算能力,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | -$\frac{π}{14}$ | B. | -$\frac{π}{7}$ | C. | $\frac{π}{14}$ | D. | $\frac{π}{7}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{5}$ | B. | $\frac{2}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| 广告费用x(万元) | 2 | 3 | 4 | 5 | 6 |
| 销售轿车y(台数) | 3 | 4 | 6 | 10 | 12 |
| A. | 17 | B. | 18 | C. | 19 | D. | 20 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如甲图所示,在矩形ABCD中,AB=4,AD=2,E是CD的中点,将△ADE沿AE折起到△D1AE位置,使平面D1AE⊥平面ABCE,得到乙图所示的四棱锥D1-ABCE.
如甲图所示,在矩形ABCD中,AB=4,AD=2,E是CD的中点,将△ADE沿AE折起到△D1AE位置,使平面D1AE⊥平面ABCE,得到乙图所示的四棱锥D1-ABCE.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | z>x>y | B. | z>y>x | C. | x>y>z | D. | x>z>y |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 单价x(元/件) | 60 | 62 | 64 | 66 | 68 | 70 |
| 销量y(件) | 91 | 84 | 81 | 75 | 70 | 67 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
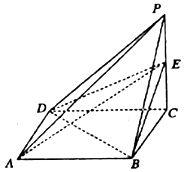 如图,已知四棱锥P-ABCD是边长为1的正方形,PB=PD=$\sqrt{5}$,PC=2,E是侧棱PC上的动点.
如图,已知四棱锥P-ABCD是边长为1的正方形,PB=PD=$\sqrt{5}$,PC=2,E是侧棱PC上的动点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com