
(12分)已知函数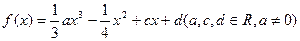 满足
满足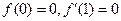 ,且
,且 在
在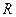 上单调递增.
上单调递增.
(1)求 的解析式;
的解析式;
(2)若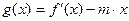 在区间
在区间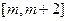 上的最小值为
上的最小值为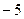 ,求实数
,求实数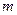 的值.
的值.
科目:高中数学 来源: 题型:解答题
(本题满分12分)某网民用电脑上因特网有两种方案可选:一是在家里上网,费用分为通讯费(即电话费)与网络维护费两部分。现有政策规定:通讯费为0.02元/分钟,但每月30元封顶(即超过30元则只需交30元),网络维护费1元/小时,但每月上网不超过10小时则要交10元;二是到附近网吧上网,价格为1.5元/小时。
(1)将该网民在某月内在家上网的费用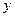 (元)表示为时间
(元)表示为时间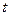 (小时)的函数;
(小时)的函数;
(2)试确定在何种情况下,该网民在家上网更便宜?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分12分)已知函数f(x)=2x-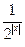 .
.
(1)若f(x)=2,求x的值;
(2)若2tf(2t)+mf(t)≥0对于t∈[1,2]恒成立,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分12分)函数 的定义域为
的定义域为 (
(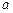 为实数).
为实数).
(1)当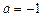 时,求函数
时,求函数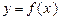 的值域;
的值域;
(2)若函数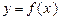 在定义域上是减函数,求
在定义域上是减函数,求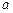 的取值范围;
的取值范围;
(3)函数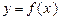 在
在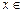
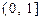 上的最大值及最小值,并求出函数取最值时
上的最大值及最小值,并求出函数取最值时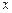 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(14分)某公司生产一种产品的固定成本为0.5万元,但每生产100件需再增加成本0.25万元,市场对此产品的年需求量为500件,年销售收入(单位:万元)为R(t)=5t-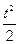 (0≤t≤5),其中t为产品售出的数量(单位:百件).
(0≤t≤5),其中t为产品售出的数量(单位:百件).
(1)把年利润表示为年产量x(百件)(x≥0)的函数f(x);
(2)当年产量为多少件时,公司可获得最大年利润?
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
函数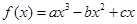 的图象如图所示,且
的图象如图所示,且 在
在 与
与 处取得极值,给出下列判断:
处取得极值,给出下列判断: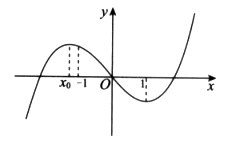
①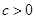 ;
;
②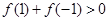 ;
;
③函数 在区间
在区间 上是增函数。
上是增函数。
其中正确的判断是( )
| A.①③ | B.② | C.②③ | D.①② |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com