练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】若一个三位数的个位数字大于十位数字，十位数字大于百位数字，我们就称这个三位数为“递增三位数”.现从所有的递增三位数中随机抽取一个，则其三个数字依次成等差数列的概率为__________．

    【答案】；

    【解析】

    利用列举法列举出所有符合“递增三位数”的三位数,并找出符合等差数列的个数,即可由古典概型概率的计算公式求解.

    根据定义“递增三位数”, 个位数字大于十位数字,十位数字大于百位数字.可知个位数最小为3,最大为9

    当个位数为3时,三位数为,共1个.三个数字依次成等差数列的有1个.

    当个位数为4时,三位数为,共3个.三个数字依次成等差数列的为,有1个

    当个位数为5时,三位数为,共6个.三个数字成等差数列的为有2个.

    当个位数为6时,三位数为共10个.三个数字成等差数列的为,有2个.

    当个位数为7时,三位数为共15个,三个数字成等差数列的为,有3个.

    当个位数为8时,三位数为,.共21个, 三个数字成等差数列的为,有3个.

    当个位数为9时,三位数为,,,,,,共个, 三个数字成等差数列的为,有4个.

    综上可知, “递增三位数”共有个.三个数字成等差数列的共有个

    则从所有的递增三位数中随机抽取一个,则其三个数字依次成等差数列的概率为

    故答案为:

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】通过随机询问某地100名高中学生在选择座位时是否挑同桌，得到如下列联表：

    男生

    女生

    合计

    挑同桌

    30

    40

    70

    不挑同桌

    20

    10

    30

    总计

    50

    50

    100

    （1）从这50名男生中按是否挑同桌采取分层抽样的方法抽取一个容量为5的样本，现从这5名学生中随机选取3名做深度采访，求这3名学生中恰有2名挑同桌的概率；

    （2）根据以上列联表，是否有以上的把握认为“性别与在选择座位时是否挑同桌”有关？

    下面的临界值表供参考：

    0.050

    0.010

    0.001

    3.841

    6.635

    10.828

    （参考公式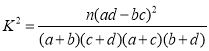：，其中.）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】随着网络的发展，网上购物越来越受到人们的喜爱，各大购物网站为增加收入，促销策略越来越多样化，促销费用也不断增加.下表是某购物网站2018年1月～8月促销费用（万元）和产品销量（万件）的具体数据.

    月份

    1

    2

    3

    4

    5

    6

    7

    8

    促销费用

    2

    3

    6

    10

    13

    21

    15

    18

    产品销量

    1

    1

    2

    3

    3.5

    5

    4

    4.5

    （1）根据数据可知与具有线性相关关系，请建立与的回归方程（系数精确到0.01）；

    （2）已知6月份该购物网站为庆祝成立1周年，特制定奖励制度：以（单位：件）表示日销量，，则每位员工每日奖励100元；，则每位员工每日奖励150元，，则每位员工每日奖励200元.现已知该网站6月份日销量服从正态分布，请你计算某位员工当月奖励金额总数大约多少元（当月奖励金额总数精确到百分位）.

    参考数据：，，其中，分别为第个月的促销费用和产品销量，.

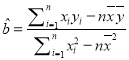    参考公式：①对于一组数据，，…，，其回归方程的斜率和截距的最小二乘估计分别为，；②若随机变量服从正态分布，则，.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知椭圆的焦距为2，过点.

    （1）求椭圆的标准方程；

    （2）设椭圆的右焦点为F，定点，过点F且斜率不为零的直线l与椭圆交于A，B两点，以线段AP为直径的圆与直线的另一个交点为Q，证明：直线BQ恒过一定点，并求出该定点的坐标.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

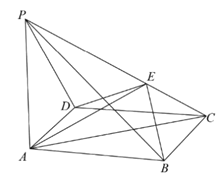
    【题目】如图，在四棱锥中，底面为正方形，平面，，为上异于的点.

    （1）求证：平面平面；

    （2）当与平面所成角为时，求的长；

    （3）当时，求二面角的余弦值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某大型公司为了切实保障员工的健康安全，贯彻好卫生防疫工作的相关要求，决定在全公司范围内举行一次乙肝普查.为此需要抽验960人的血样进行化验，由于人数较多，检疫部门制定了下列两种可供选择的方案.

    方案①：将每个人的血分别化验，这时需要验960次.

    方案②：按个人一组进行随机分组，把从每组个人抽来的血混合在一起进行检验，如果每个人的血均为阴性，则验出的结果呈阴性，这个人的血就只需检验一次（这时认为每个人的血化验一次）；否则，若呈阳性，则需对这个人的血样再分别进行一次化验.这样，该组个人的血总共需要化验次.

    假设此次普查中每个人的血样化验呈阳性的概率为，且这些人之间的试验反应相互独立.

    （1）设方案②中，某组个人中每个人的血化验次数为，求的分布列；

    （2）设.试比较方案②中，分别取2，3，4时，各需化验的平均总次数；并指出在这三种分组情况下，相比方案①，化验次数最多可以平均减少多少次？（最后结果四舍五入保留整数）.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知椭圆：的离心率，且圆过椭圆的上，下顶点.

    （1）求椭圆的方程.

    （2）若直线的斜率为，且直线交椭圆于、两点，点关于点的对称点为，点是椭圆上一点，判断直线与的斜率之和是否为定值，如果是，请求出此定值：如果不是，请说明理.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设数列是公差不为零等差数列，满足；数列的前项和为，且满足.

    （1）求数列、的通项公式；

    （2）在和之间插入1个数，使成等差数列；在和之间插入2个数，使成等差数列；……；在和之间插入个数，使成等差数列，

    （i）求；

    （ii）是否存在正整数，使成立？若存在，求出所有的正整数对；若不存在，请说明理由.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数．

    (1)若，求函数的所有零点；

    (2)若，证明函数不存在极值．

    查看答案和解析>>

    同步练习册答案