
 ij���й�˾��Ʊ��30����ÿ�ɵĽ��۸�p��Ԫ����ʱ��t���죩����������ԣ�t��p�����㣨t��p��������ͼ�е������߶��ϣ��ù�Ʊ��30���ڣ�����30�죩�Ľ�����q����Ԫ����ʱ��t���죩�IJ������������ʾ��
ij���й�˾��Ʊ��30����ÿ�ɵĽ��۸�p��Ԫ����ʱ��t���죩����������ԣ�t��p�����㣨t��p��������ͼ�е������߶��ϣ��ù�Ʊ��30���ڣ�����30�죩�Ľ�����q����Ԫ����ʱ��t���죩�IJ������������ʾ��| ��t�� | 4 | 10 | 16 | 22 |
| q����ɣ� | 26 | 20 | 14 | 8 |
���� ��1���ɿ���0��t��20ʱ��p��t����һ�κ�����ϵ���Ӷ���p=at+b����ͼ�����㣨0��2������20��6�����������ʽ������a��b����ͬ���������20��t��30ʱ��p��t������ϵʽ���Ӷ��ó�$p=\left\{\begin{array}{l}{\frac{1}{5}t+2}&{0��t��20}\\{-\frac{1}{10}t+8}&{20��t��30}\end{array}\right.$��
��2������t��q����һ�κ�����ϵʽ���Ӷ�����q=kt+m���ɱ�������֪�ú���ͼ����㣨4��26������10��20�����Ӷ��������k��m���Ӷ��ó�q=-t+30��
��3���������⼴�ɵó�y=$\left\{\begin{array}{l}{-\frac{1}{5}��t-10��^{2}+80}&{0��t��20}\\{\frac{1}{10}��t-55��^{2}-\frac{125}{2}}&{20��t��30}\end{array}\right.$�������������ÿ����y�����ֵ���Ƚϼ��������30���еڼ��ս�������Լ����ֵΪ���٣�
��� �⣺��1����0��t��20ʱ����p=at+b����ͼ���֪���㣨0��2������20��6��������ã�
$\left\{\begin{array}{l}{2=b}\\{6=20a+b}\end{array}\right.$�����$\left\{\begin{array}{l}{b=2}\\{a=\frac{1}{5}}\end{array}\right.$��
��$p=\frac{1}{5}t+2$��
ͬ���ɵõ�20��t��30ʱ$p=-\frac{1}{10}t+8$��
���Ͽɵ�$p=\left\{\begin{array}{l}{\frac{1}{5}t+2}&{0��t��20}\\{-\frac{1}{10}t+8}&{20��t��30}\end{array}\right.$��
��2����������q=kt+m�����㣨4��26������10��20�����ɵã�
$\left\{\begin{array}{l}{26=4k+m}\\{20=10k+m}\end{array}\right.$�����$\left\{\begin{array}{l}{k=-1}\\{m=30}\end{array}\right.$��
��q=-t+30��
��3��������ɵ�$y=pq=\left\{\begin{array}{l}{��\frac{1}{5}t+2����-t+30��}&{0��t��20}\\{��-\frac{1}{10}t+8����-t+30��}&{20��t��30}\end{array}\right.$=$\left\{\begin{array}{l}{-\frac{1}{5}��t-10��^{2}+80}&{0��t��20}\\{\frac{1}{10}��t-55��^{2}-\frac{125}{2}}&{20��t��30}\end{array}\right.$��
�൱0��t��20ʱ��t=10ʱ��ymax=80��Ԫ��
��20��t��30ʱ��t=20ʱ��ymax=60��Ԫ��
���Ͽɵõ�10�յĽ������Ϊ80��Ԫ��
���� �������ϵ����������ʽ�ķ������Լ�һ�κ�����һ����ʽ��ͼ���ϵĵ������ͺ�������ʽ�Ĺ�ϵ���Լ��䷽������κ�������ֵ���ֶκ�����ֵ����



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��֪�����ABECD��һ��ֱ������ABCD��һ���ȱ�������BCE���ɣ���ͼ1��ʾ��AB��BC����AB=2BC=2CD��������ABCD����BC�����γ���ͼ2��ʾ�ļ����壬��AB��ƽ��BEC��
��֪�����ABECD��һ��ֱ������ABCD��һ���ȱ�������BCE���ɣ���ͼ1��ʾ��AB��BC����AB=2BC=2CD��������ABCD����BC�����γ���ͼ2��ʾ�ļ����壬��AB��ƽ��BEC���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
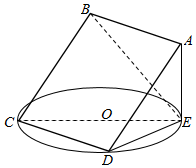 ��ͼ��ʾ��������ABCD����ƽ����ԲO����ƽ���ཻ��CD���߶�CDΪԲO���ң�AE��ֱ��ԲO����ƽ�棬����E��ԲO������C��D�ĵ㣬AE=3��ԲO��ֱ��Ϊ9��
��ͼ��ʾ��������ABCD����ƽ����ԲO����ƽ���ཻ��CD���߶�CDΪԲO���ң�AE��ֱ��ԲO����ƽ�棬����E��ԲO������C��D�ĵ㣬AE=3��ԲO��ֱ��Ϊ9���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | a��0 | B�� | a��-2 | C�� | a��-$\frac{5}{2}$ | D�� | a��-3 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com