练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    16．在二项式（9x-$\frac{1}{{3\root{3}{x}}}}$）n的展开式中，偶数项的二项式系数之和为256，则展开式中x的系数为84．

    分析 根据二项式展开式中，偶数项与奇数项的二项式系数之和相等，求出n的值；再利用二项展开式的通项公式，即可求出展开式中x的系数．

    解答 解：二项式展开式中，偶数项与奇数项的二项式系数之和相等，
    所以2n-1=256，解得n=9；
    所以二项式（9x-$\frac{1}{{3\root{3}{x}}}}$）9的展开式中，通项公式为
    Tr+1=${C}_{9}^{r}$•（9x）9-r•${（-\frac{1}{3\root{3}{x}}）}^{r}$=${C}_{9}^{r}$•99-r•${（-\frac{1}{3}）}^{r}$•${x}^{9-\frac{4γ}{3}}$；
    令9-$\frac{4r}{3}$=1，解得r=6；
    所以展开式中x的系数为
    ${C}_{9}^{6}$•93•${（-\frac{1}{3}）}^{6}$=84．
    故答案为：84．

    点评 本题考查了二项式展开式的二项式系数的应用问题，也考查了二项式展开式的通项公式应用问题，是基础题目．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    6．袋中有6个红球，4个白球，从中任取1球，记住颜色后再放回，连续摸取4次，设X为取得红球的次数，则X的方差D（X）的值为（　　）
    A．$\frac{12}{5}$B．$\frac{24}{25}$C．$\frac{8}{5}$D．$\frac{2\sqrt{6}}{5}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    7．如图所示的正数数阵中，第一横行是公差为d的等差数列，各列均是公比为q等比数列，已知a1，1=1，a1，4=7，a4，1=$\frac{1}{8}$，则下列结论中不正确的是（　　）
    A．d+2q=a1，2B．a2，1+a2，3+a2，5+…+a2，21=$\frac{441}{2}$
    C．每一横行都是等差数列D．ai，j=（2j-1）+21-i（i，j均为正整数）

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    4．已知函数f（x）=$\frac{1}{2}$x2+ax-2xlnx（a∈R）．
    （1）当a=5时，判断g（x）=f（x）-$\frac{1}{2}$x2在[1，e]上的单调性并加以证明；
    （2）当a=4-e时，试探讨函数f（x）在（0，+∞）上是否存在极小值？，若存在，求出极小值；若不存在，请说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

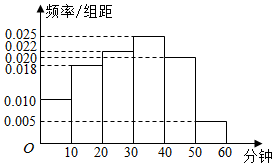    11．某中学为研究学生的身体素质与课外体育锻炼时间的关系，对该校200名学生的课外体育锻炼平均每天运动的时间（单位：分钟）进行调查，将收集到的数据分成[0，10），[10，20），[20，30），[30，40），[40，50），[50，60）六组，并作出频率分布直方图（如图）．将日均课外体育锻炼时间不低于40分钟的学生评价为“课外体育达标”．
    （1）请根据直方图中的数据填写下面的2×2列联表，并通过计算判断是否能在犯错误的概率不超过0.01的前提下认为“课外体育达标”与性别有关？
    课外体育不达标课外体育达标合计
    男603090
    女9020110
    合计15050200
    （2）现按照“课外体育达标”与“课外体育不达标”进行分层抽样，抽取12人，再从这12名学生中随机抽取3人参加体育知识问卷调查，记“课外体育达标”的人数为ξ，求ξ得分布列和数学期望．
    附参考公式与数据：K2=$\frac{n（{ad-bc）}^{2}}{（a+b）（c+d）（a+c）（b+d）}$
    P（K2≥k0）0.100.050.0100.0050.001
    k02.7063.8416.6357.87910.828

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

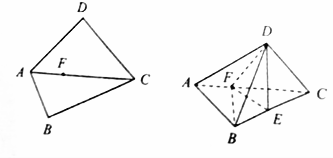    1．如图，平面四边形ABCD中，∠B=∠D=90°，AC=2AB=4$\sqrt{3}$，DA=DC，F是AC上一点，且AF=$\frac{1}{3}$AC．将该四边形沿AC折起，使点D在平面ABC的射影E恰在BC上，此时DE=2$\sqrt{2}$．
    （Ⅰ）证明：AB⊥平面BCD；
    （Ⅱ）证明：AB∥平面DEF；
    （Ⅲ）求三棱锥A-BDF的体积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    8．用反余弦函数值的形式表示各式中的x：
    （1）cosx=$\frac{3}{4}$，x∈[0，π]；
    （2）cosx=-$\frac{\sqrt{5}}{5}$，x∈[0，π]；
    （3）cosx=-$\frac{\sqrt{5}}{5}$，x∈[-π，0]；
    （4）cosx=$\frac{3}{4}$，x∈[-$\frac{π}{2}$，0]；
    （5）cosx=$\frac{3}{4}$，x∈[$\frac{3π}{2}$，2π]；
    （6）cosx=$\frac{3}{4}$，x∈[-$\frac{π}{2}$，$\frac{π}{2}$]；
    （7）cosx=-$\frac{\sqrt{5}}{5}$，x∈[$\frac{1}{2}$π，$\frac{3}{2}$π]．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    5．若将函数f（x）=（x-1）7表示为f（x）=a0+a1（x+1）+a2（x+1）2+…+a7（x+1）7，其中（ai∈R，i=0，1，2，…，7）为实数，则a4等于-280．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    6．如图，在直四棱柱ABCD-A1B1C1D1中，底面ABCD为等腰梯形，AB∥CD，AB=4，BC=CD=2，AA1=2，E，E1分别是棱AD，AA1的中点．
    （1）设F是棱AB的中点，证明：直线EE1∥平面FCC1；
    （2）证明：平面D1AC⊥平面BB1C1C；
    （3）求点D到平面D1AC的距离．

    查看答案和解析>>

    同步练习册答案