
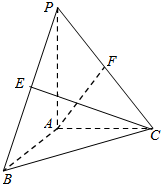
 (理科做)如图,在三棱锥P-ABC中,已知PA⊥平面ABC,∠BAC=$\frac{π}{2}$,PA=AB=AC,E,F分别为棱PB,PC的中点,则异面直线AF与CE所成的角的余弦值为$\frac{\sqrt{3}}{6}$.
(理科做)如图,在三棱锥P-ABC中,已知PA⊥平面ABC,∠BAC=$\frac{π}{2}$,PA=AB=AC,E,F分别为棱PB,PC的中点,则异面直线AF与CE所成的角的余弦值为$\frac{\sqrt{3}}{6}$. 分析 以A为原点,AB为x轴,AC为y轴,AP为z轴,建立空间直角坐标系,利用向量法能求出异面直线AF与CE所成的角的余弦值.
解答 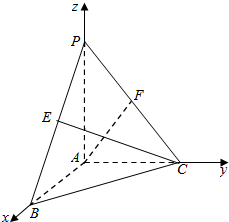 解:∵在三棱锥P-ABC中,PA⊥平面ABC,∠BAC=$\frac{π}{2}$,
解:∵在三棱锥P-ABC中,PA⊥平面ABC,∠BAC=$\frac{π}{2}$,
∴以A为原点,AB为x轴,AC为y轴,AP为z轴,建立空间直角坐标系,
设PA=AB=AC=2,
∵E,F分别为棱PB,PC的中点,
∴A(0,0,0),B(2,0,0),P(0,0,2),E(1,0,1),
C(0,2,0),F(0,1,1),
$\overrightarrow{AF}$=(0,1,1),$\overrightarrow{CE}$=(1,-2,1),
设异面直线AF与CE所成的角为θ,
cosθ=$\frac{|\overrightarrow{AF}•\overrightarrow{CE}|}{|\overrightarrow{AF}|•|\overrightarrow{CE}|}$=$\frac{|-1|}{\sqrt{2}×\sqrt{6}}$=$\frac{\sqrt{3}}{6}$.
∴异面直线AF与CE所成的角的余弦值为$\frac{\sqrt{3}}{6}$.
故答案为:$\frac{\sqrt{3}}{6}$.
点评 本题考查异面直线所成角的求法,是基础题,解题时要认真审题,注意向量法的合理运用.


 智能训练练测考系列答案
智能训练练测考系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 某糖厂为了解一条自动生产线上生产袋装白糖的重量,从1000袋白糖中,随机抽取100袋并称出每袋白糖的重量(单位:g),得到如下频率分布表:
某糖厂为了解一条自动生产线上生产袋装白糖的重量,从1000袋白糖中,随机抽取100袋并称出每袋白糖的重量(单位:g),得到如下频率分布表:| 分组 | 频数 | 频率 |
| [485.5,490.5) | 10 | |
| [490.5,495.5) | 0.20 | |
| [495.5,500.5) | 50 | |
| [500.5,505.5] | ||
| 合计 | 100 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com