D
分析:再依据条件求得 f(2a)=0,f(3a)=-1,故排除A.求出函数的定义域,根据条件计算f(-x)与f(x)的关系,再根据函数的奇偶性的定义判定函数为奇函数,故排除B.
由条件求出f(x-a)=-
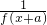
,可得 f(x)=
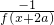
=f(x+4a),故函数是周期函数,可得D正确.求得先证明x∈(2a,3a)时,f(x)<0,再根据单调性的定义进行证明,
可得f(x)在[2a,3a]上单调递减,故排除C,综合可得结论.
解答:由f(x-y)=
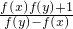
成立,且f(a)=1,可求得 f(2a)=f(a+a)=f[a-(-a)]=
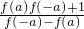
=
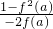
=0,
f(3a)=f(2a+a)=f[2a-(-a)]=
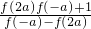
=
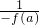
=-1,故A不正确.
∵定义域{x|x≠kπ,k∈Z}关于原点对称,f(a)=1,又f(-x)=f[(a-x)-a]=
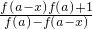
=

=

=
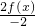
=-f(x),∴f(x)为奇函数,故B不正确.
由于 f(x-a)=
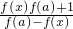
=
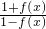
=
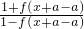
=
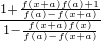
=-
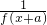
,
所以 f(x)=
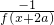
=f(x+4a),故函数f(x)为周期性等于4a的周期函数,故D正确.
先证明f(x)在[2a,3a]上单调递减,由题意可得必须证明x∈(2a,3a)时,f(x)<0.
设2a<x<3a,则0<x-2a<a,∴f(x-2a)=
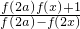
=
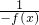
>0,∴f(x)<0.
设2a<x
1<x
2<3a,则0<x
2-x
1<a,∴f(x
1)<0f(x
2)<0,f(x
2-x
1)>0,
∴f(x
1)-f(x
2)=
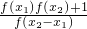
>0,∴f(x
1)>f(x
2),∴f(x)在[2a,3a]上单调递减,故C不正确.
故选D.
点评:本题主要考查了函数奇偶性和周期性的判断,以及函数的最值及其几何意义等有关知识,属于中档题.

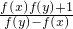 成立,且f(a)=1(a为正常数),当0<x<2a时,f(x)>0则
成立,且f(a)=1(a为正常数),当0<x<2a时,f(x)>0则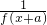 ,可得 f(x)=
,可得 f(x)=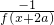 =f(x+4a),故函数是周期函数,可得D正确.求得先证明x∈(2a,3a)时,f(x)<0,再根据单调性的定义进行证明,
=f(x+4a),故函数是周期函数,可得D正确.求得先证明x∈(2a,3a)时,f(x)<0,再根据单调性的定义进行证明,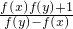 成立,且f(a)=1,可求得 f(2a)=f(a+a)=f[a-(-a)]=
成立,且f(a)=1,可求得 f(2a)=f(a+a)=f[a-(-a)]=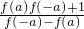 =
=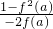 =0,
=0,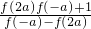 =
=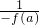 =-1,故A不正确.
=-1,故A不正确.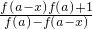
 =
= =
=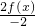 =-f(x),∴f(x)为奇函数,故B不正确.
=-f(x),∴f(x)为奇函数,故B不正确.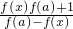 =
=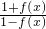 =
=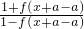 =
=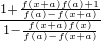 =-
=-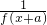 ,
,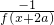 =f(x+4a),故函数f(x)为周期性等于4a的周期函数,故D正确.
=f(x+4a),故函数f(x)为周期性等于4a的周期函数,故D正确.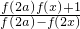 =
=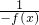 >0,∴f(x)<0.
>0,∴f(x)<0.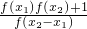 >0,∴f(x1)>f(x2),∴f(x)在[2a,3a]上单调递减,故C不正确.
>0,∴f(x1)>f(x2),∴f(x)在[2a,3a]上单调递减,故C不正确.

