解:(Ⅰ)∵f(x)=x
3+mx,∴f′(x)=3x
2+m.
①当m≥0时,f′(x)≥0恒成立,所以f(x)在(-∞,+∞)上是增函数.
②当m<0时,若f′(x)<0,则
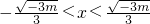
.若f′(x)>0,则x<
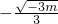
,或x>

,
所以f(x)在(-

,

)上是减函数,在(-∞,-

),(

,+∞)上是增函数;
(Ⅱ)∵F(x)=x
3+mx+nx
2+n
2,在x=1处有极值10,
∴F′(x)=3x
2+2nx+m.
∴
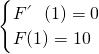
,∴
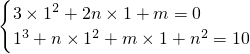
,
∴m=-11,n=4.或m=3,n=-3.
当m=3,n=-3时,F′(x)=3(x-1)
2≥0,函数F(x)在R上是增函数,所以F(x)在x=1处无极值,不合题意.
当m=-11,n=4时,F′(x)=3x
2+8x-11=(3x+11)(x-1),
当-

<x<1时,F′(x)<0;当x>1时,F′(x)>0.
∴函数F(x)在x=1处取得极小值,符合题意.
∴m=-11,n=4.∴切线方程为11x+y-16=0.
(Ⅲ)∵F(x)=x
3+mx+nx
2+n
2,
∴F′(x)=3x
2+2nx+m.
∵n
2<3m,△=4(n
2-3m)<0,∴F′(x)>0,
∴F(x)=x
3+mx+nx
2+n
2在R上是增函数.
∵F(
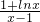
)>F(

)对任意x∈(1,+∞)恒成立,∴
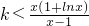
对任意x∈(1,+∞)恒成立.
设函数h(x)=
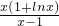
,则h′(x)=
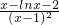
.
设m(x)=x-lnx-2,则m′(x)=1-

.
∵x∈(1,+∞),m′(x)>0,则m(x)=x-lnx-2在(1,+∞)上是增函数,
因为m(1)=-1,m(2)=-ln2,m(3)=1-ln3<0,m(4)=2-ln4>0,所以?x
0∈(3,4),使m(x
0)=x
0-lnx
0-2=0
所以x∈(1,x
0)时,m(x)<0,h′(x)<0,所以h(x)=
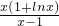
在(1,+∞)上递减,
x∈(x
0,+∞)时,m(x)>0,h′(x)>0,所以h(x)=
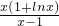
在(x
0,+∞)上递增,
所以h(x)的最小值为h(x
0)=
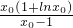
,
又因为m(x
0)=x
0-lnx
0-2=0,所以h(x
0)=x
0,
因为x
0∈(3,4),且k<h(x)对任意x∈(1,+∞)恒成立,所以k<h(x)
min,
所以k≤3,整数k的最大值为3.
分析:(Ⅰ)求f′(x),解含参数m的不等式f′(x)>0,f′(x)<0即可;
(Ⅱ)由函数F(x)在x=l处有极值为10,可得F′(1)=0,F(1)=10,由此可求出F(x),由导数的几何意义及直线点斜式方程可求切线方程;
(Ⅲ)由n
2<3m,可得F(x)为增函数,从而不等式
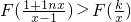
可转化为
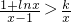
,分离出参数k,转化为函数最值问题即可解决.
点评:本题考查导数的几何意义、应用导数研究函数的单调性及函数恒成立问题,属于导数的综合应用,有一定难度,特别是恒成立问题,常常转化为函数最值问题,进而可用导数解决.

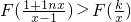 对?x∈(1,+∞)恒成立,求整数k的最大值.
对?x∈(1,+∞)恒成立,求整数k的最大值.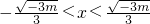 .若f′(x)>0,则x<
.若f′(x)>0,则x<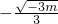 ,或x>
,或x> ,
, ,
, )上是减函数,在(-∞,-
)上是减函数,在(-∞,- ),(
),( ,+∞)上是增函数;
,+∞)上是增函数;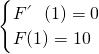 ,∴
,∴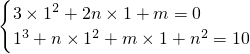 ,
, <x<1时,F′(x)<0;当x>1时,F′(x)>0.
<x<1时,F′(x)<0;当x>1时,F′(x)>0.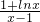 )>F(
)>F( )对任意x∈(1,+∞)恒成立,∴
)对任意x∈(1,+∞)恒成立,∴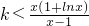 对任意x∈(1,+∞)恒成立.
对任意x∈(1,+∞)恒成立.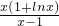 ,则h′(x)=
,则h′(x)=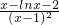 .
. .
.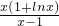 在(1,+∞)上递减,
在(1,+∞)上递减,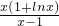 在(x0,+∞)上递增,
在(x0,+∞)上递增,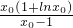 ,
,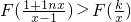 可转化为
可转化为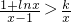 ,分离出参数k,转化为函数最值问题即可解决.
,分离出参数k,转化为函数最值问题即可解决.

 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案 已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<