下列四个命题:①“等边三角形的三个内角均为60° 的逆命题,②“若k＞0.则方程x2+2x-k=0有实根的逆否命题,③“全等三角形的面积相等的否命题,④“若$\overrightarrow a$•$\overrightarrow b$=$\overrightarrow a$•$\overrightarrow c$.则$\overrightarrow 题目和参考答案——青夏教育精英家教网—

精英家教网 > 高中数学 > 题目详情

17．下列四个命题：
①“等边三角形的三个内角均为60°”的逆命题；
②“若k＞0，则方程x²+2x-k=0有实根”的逆否命题；
③“全等三角形的面积相等”的否命题；
④“若$\overrightarrow a$•$\overrightarrow b$=$\overrightarrow a$•$\overrightarrow c$，则$\overrightarrow a$⊥$（\overrightarrow b-\overrightarrow c）$”的否命题，
其中真命题的个数是（　　）

A．

B．

C．

D．

分析 ①利用逆命题的意义即可得出，再利用等边三角形的定义即可得出；
②利用逆否命题的定义即可得出，再利用一元二次方程的是否有实数根与判别式的关系即可得出；
③利用否命题的意义即可得出，进而判断出真假
④根据向量垂直数量积为判定．

解答解：对于①“等边三角形的三个内角均为60°”的逆命题是“三个内角均为60的三角形是等边三角形”是真命题；
对于②，∵方程x²+2x-k=0无实根时△=4+4k＜0，即k＜-1”，∴原命题的逆否命题“若方程x²+2x-k=0无实根，则k＜0”是真命题；
对于③“全等三角形的面积相等”的否命题是“不全等三角形的面积不相等”，故错；
对于④“若$\overrightarrow a$•$\overrightarrow b$=$\overrightarrow a$•$\overrightarrow c$，则$\overrightarrow a$⊥$（\overrightarrow b-\overrightarrow c）$”的否命题是“若$\overrightarrow a$•$\overrightarrow b$≠$\overrightarrow a$•$\overrightarrow c$，则$\overrightarrow a$不垂直$（\overrightarrow b-\overrightarrow c）$”是真命题，
故选：D．

点评本题考查了命题的四种形式及真假关系，属于基础题．

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源： 题型：选择题

7．

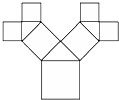如图所示，正方形上连接着等腰直角三角形，等腰直角三角形边上再连接正方形…，如此继续，若共得到1023个正方形，设初始正方形的边长为$\frac{{\sqrt{2}}}{2}$，则最小正方形的边长为（　　）

A．

$\frac{1}{64}$

B．

$\frac{1}{16}$

C．

$\frac{1}{32}$

D．

$\frac{1}{8}$

查看答案和解析>>

科目：高中数学 来源： 题型：选择题

8．已知集合U=R，A={x|-1＜x＜10}，B={x|x-4≥0}，则A∩∁_UB=（　　）

A．

{x|-1＜x＜4}

B．

{x|-1＜x≤4}

C．

{x|4≤x＜10}

D．

{x|-1≤x≤4}

查看答案和解析>>

科目：高中数学 来源： 题型：解答题

5．在平面直角坐标系xOy中，直线3x-y+$\sqrt{5}$=0截以原点O为圆心的圆所得的弦长为$\sqrt{14}$
（1）求圆O的方程；
（2）若直线l与圆O切于第一象限，且与坐标轴交于点D、E，当DE长最小时，求直线l的方程；
（3）设M、P是圆O上任意两点，点M关于x轴的对称点为N，若直线MP、NP分别交x轴于点（m，0）和（n，0），问mn是否为定值？若是，请求出该定值；若不是，请说明理由．

查看答案和解析>>

科目：高中数学 来源： 题型：填空题

12．函数f（x）=x²-2ax+2的单调减区间为（-∞，4]，则a=4．

查看答案和解析>>

科目：高中数学 来源： 题型：选择题

2．若a＜0，则$\sqrt{a{x^3}}$=（　　）

A．

x$\sqrt{ax}$

B．

x$\sqrt{-ax}$

C．

-x$\sqrt{-ax}$