
分析 (1)由点O到直线3x-y+$\sqrt{5}$=0的距离d,求出圆O的半径r,写出圆O的方程;
(2)写出直线l的方程,由d=r以及基本不等式求出DE2取最小值时对应的方程;
(3)设出点M、P,根据对称性写出点N,利用圆的方程表示出直线MP、
NP与x轴的交点坐标,得出m、n的值,计算mn即可.
解答 解:(1)因为点O到直线3x-y+$\sqrt{5}$=0的距离为
d=$\frac{|3×0-1×0+\sqrt{5}|}{\sqrt{{3}^{2}{+(-1)}^{2}}}$=$\frac{1}{\sqrt{2}}$,
所以圆O的半径为r=$\sqrt{{(\frac{1}{\sqrt{2}})}^{2}{+(\frac{\sqrt{14}}{2})}^{2}}$=2;…(2分)
故圆O的方程为x2+y2=4;…(4分)
(2)设直线l的方程为$\frac{x}{a}$+$\frac{y}{b}$=1(a>0,b>0),
即bx+ay-ab=0;
由已知$\frac{|0+0-ab|}{\sqrt{{b}^{2}{+a}^{2}}}$=2,
即$\frac{1}{{a}^{2}}$+$\frac{1}{{b}^{2}}$=$\frac{1}{4}$;…(6分)
所以DE2=a2+b2
=4(a2+b2)($\frac{1}{{a}^{2}}$+$\frac{1}{{b}^{2}}$)
=4(2+$\frac{{b}^{2}}{{a}^{2}}$+$\frac{{a}^{2}}{{b}^{2}}$)≥16; …(9分)
当且仅当a=b=2$\sqrt{2}$时取等号,
此时直线l的方程为x+y-2$\sqrt{2}$=0;…(10分)
(3)设点M(x1,y1),P(x2,y2),
则N(x1,-y1),且${{x}_{1}}^{2}$+${{y}_{1}}^{2}$=4${{x}_{2}}^{2}$+${{y}_{2}}^{2}$=4,
直线MP与x轴交点为($\frac{{{x}_{1}y}_{2}{{-x}_{2}y}_{1}}{{y}_{2}{-y}_{1}}$,0),
则m=$\frac{{{x}_{1}y}_{2}{{-x}_{2}y}_{1}}{{y}_{2}{-y}_{1}}$; …(12分)
直线NP与x轴交点为($\frac{{{x}_{1}y}_{2}{{+x}_{2}y}_{1}}{{y}_{2}{+y}_{1}}$,0),
则n=$\frac{{{x}_{1}y}_{2}{{+x}_{2}y}_{1}}{{y}_{2}{+y}_{1}}$.…(14分)
所以mn=$\frac{{{x}_{1}y}_{2}{{-x}_{2}y}_{1}}{{y}_{1}{-y}_{2}}$•$\frac{{{x}_{1}y}_{2}{{+x}_{2}y}_{1}}{{y}_{2}{+y}_{1}}$
=$\frac{{{{{x}_{1}}^{2}y}_{2}}^{2}{{{{-x}_{2}}^{2}}_{{y}_{1}}}^{2}}{{{y}_{2}}^{2}{{-y}_{1}}^{2}}$
=$\frac{(4{{-y}_{1}}^{2}{{)y}_{2}}^{2}-(4{{-y}_{2}}^{2}{{)y}_{1}}^{2}}{{{y}_{2}}^{2}{{-y}_{1}}^{2}}$=4,
故mn为定值4.…(16分)
点评 本题考查了直线与圆位置关系的应用问题,也考查了点到直线距离的应用问题以及求最值的应用问题,是综合性题目.


科目:高中数学 来源: 题型:解答题
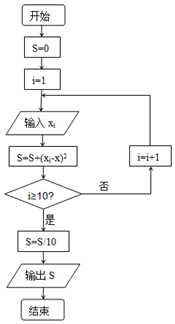 三月植树节,林业管理部门在植树前,为了保证树苗的质量,都会在植树前对树苗进行检测,现从甲、乙两种树苗中各抽测了10株树苗,量出它们的高度如下(单位:厘米):
三月植树节,林业管理部门在植树前,为了保证树苗的质量,都会在植树前对树苗进行检测,现从甲、乙两种树苗中各抽测了10株树苗,量出它们的高度如下(单位:厘米):查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | $\frac{1}{4}$ | C. | -4 | D. | $-\frac{1}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{2}$ | B. | 2 | C. | $\sqrt{2}$-1 | D. | 1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com