
| A. | $({-∞,\frac{1}{e}})$ | B. | $({0,\frac{1}{e}})$ | C. | (-∞,0) | D. | (0,+∞) |
分析 函数f(x)=aex-x-2a的导函数f′(x)=aex-1,
当a≤0时,f′(x)≤0恒成立,函数f(x)在R上单调,不可能有两个零点;
当a>0时,令f′(x)=0,得x=ln$\frac{1}{a}$,函数在(-∞,ln$\frac{1}{a}$)递减,在(ln$\frac{1}{a}$,+∞)递增,
f(x)的最小值为f(ln$\frac{1}{a}$)=1-ln$\frac{1}{a}$-2a=1+lna-2a<0即可,
解答 解:函数f(x)=aex-x-2a的导函数f′(x)=aex-1,
当a≤0时,f′(x)≤0恒成立,函数f(x)在R上单调,不可能有两个零点;
当a>0时,令f′(x)=0,得x=ln$\frac{1}{a}$,函数在(-∞,ln$\frac{1}{a}$)递减,在(ln$\frac{1}{a}$,+∞)递增,
所以f(x)的最小值为f(ln$\frac{1}{a}$)=1-ln$\frac{1}{a}$-2a=1+lna-2a,
令g(a)=1+lna-2a,(a>0),g′(a)=$\frac{1}{a}-2$,a$∈(0,\frac{1}{2})$,g(a)递增,a$∈(\frac{1}{2},+∞)$递减,
∴$;g(a)_{max}=g(\frac{1}{2})=-ln2<0$$g(a)_{max}=g(\frac{1}{2})=-ln2<0$
∴f(x)的最小值为f(ln$\frac{1}{a}$)<0,函数f(x)=aex-x-2a有两个零点;
综上实数a的取值范围是:(0,+∞),
故选:D.
点评 本题考查了函数零点的个数与函数图象和横轴交点的转换,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
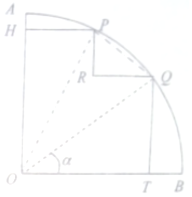 现有一圆心角为$\frac{π}{2}$,半径为12cm的扇形铁皮(如图).P,Q是弧AB上的动点且劣弧$\widehat{PQ}$的长为2πcm,过P,Q分别作与OA,OB平行或垂直的线,从扇形上裁剪出多边形OHPRQT,将该多边形面积表示为角α的函数,并求出其最大面积是多少?
现有一圆心角为$\frac{π}{2}$,半径为12cm的扇形铁皮(如图).P,Q是弧AB上的动点且劣弧$\widehat{PQ}$的长为2πcm,过P,Q分别作与OA,OB平行或垂直的线,从扇形上裁剪出多边形OHPRQT,将该多边形面积表示为角α的函数,并求出其最大面积是多少?查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 向左平移$\frac{π}{4}$个单位长度 | B. | 向右平移$\frac{π}{4}$个单位长度 | ||
| C. | 向左平移$\frac{π}{2}$个单位长度 | D. | 向右平移$\frac{π}{2}$个单位长度 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | $2\sqrt{5}$ | C. | $4\sqrt{2}$ | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $m<\frac{1}{4}$ | B. | m≤-2 | C. | $-2≤m<\frac{1}{4}$ | D. | m>2 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com