
【题目】已知函数f(x)=xlnx![]() x2﹣ax+1.
x2﹣ax+1.
(1)设g(x)=f′(x),求g(x)的单调区间;
(2)若f(x)有两个极值点x1,x2,求证:x1+x2>2.
【答案】(1)g(x)的单调递增区间为(0,1),单调递减区间为(1,+∞);(2)见解析
【解析】
(1)先得到![]() 解析式,然后对
解析式,然后对![]() 求导,分别解
求导,分别解![]() 和
和![]() ,得到其单调增区间和单调减区间;(2)由题可知x1,x2是g(x)的两零点,要证x1+x2>2,只需证x2>2﹣x1>1,只需证g(2﹣x1)>g(x2)=0,设h(x)=ln(2﹣x)﹣lnx+2x﹣2,利用导数证明
,得到其单调增区间和单调减区间;(2)由题可知x1,x2是g(x)的两零点,要证x1+x2>2,只需证x2>2﹣x1>1,只需证g(2﹣x1)>g(x2)=0,设h(x)=ln(2﹣x)﹣lnx+2x﹣2,利用导数证明![]() 在(0,1)上单调递减,从而证明
在(0,1)上单调递减,从而证明![]() ,即g(2﹣x1)>g(x2),从而证明x1+x2>2.
,即g(2﹣x1)>g(x2),从而证明x1+x2>2.
(1)∵f(x)=xlnx![]() x2﹣ax+1,
x2﹣ax+1,
∴g(x)=f'(x)=lnx﹣x+1﹣a(x>0),
∴g'(x)![]()
令g'(x)=0,则x=1,
∴当x>1时,g'(x)<0;当0<x<1时,g'(x)>0,
∴g(x)的单调递增区间为(0,1),单调递减区间为(1,+∞);
(2)∵f(x)有两个极值点x1,x2,
∴x1,x2是g(x)的两零点,
则g(x1)=g(x2)=0,
不妨设0<x1<1<x2,
∴由g(x1)=0可得a=lnx1﹣x1+1,
∵g(x)在(1,+∞)上是减函数,
∴要证x1+x2>2,只需证x2>2﹣x1>1,
只需证g(2﹣x1)>g(x2)=0,
∵g(2﹣x1)=ln(2﹣x1)﹣2+x1+1﹣(lnx1﹣x1+1)=ln(2﹣x1)﹣lnx1+2x1﹣2,
令h(x)=ln(2﹣x)﹣lnx+2x﹣2(0<x<1),
则![]() ,
,
∴h(x)在(0,1)上单调递减,
∴h(x)>h(1)=0,g(2﹣x1)>0成立,
即g(2﹣x1)>g(x2)
∴x1+x2>2.


科目:高中数学 来源: 题型:
【题目】设点![]() 的坐标分别为
的坐标分别为![]() ,直线
,直线![]() 相交于点
相交于点![]() ,且它们的斜率之积是
,且它们的斜率之积是![]() .
.
(1)求点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)直线![]() 与曲线
与曲线![]() 相交于
相交于![]() 两点,若
两点,若![]() 是否存在实数
是否存在实数![]() ,使得
,使得![]() 的面积为
的面积为![]() ?若存在,请求出
?若存在,请求出![]() 的值;若不存在,请说明理由。
的值;若不存在,请说明理由。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() 其中P,M是非空数集.记f(P)={y|y=f(x),x∈P},f(M)={y|y=f(x),x∈M}.
其中P,M是非空数集.记f(P)={y|y=f(x),x∈P},f(M)={y|y=f(x),x∈M}.
(Ⅰ)若P=[0,3],M=(﹣∞,﹣1),求f(P)∪f(M);
(Ⅱ)若P∩M=,且f(x)是定义在R上的增函数,求集合P,M;
(Ⅲ)判断命题“若P∪M≠R,则f(P)∪f(M)≠R”的真假,并加以证明.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】脐橙营养丰富,含有人体所必需的各类营养成份,若规定单个脐橙重量(单位:千克)在[0.1,0.3)的脐橙是“普通果”,重量在[0.3,0.5)的磨橙是“精品果”,重量在[0.5,0.7]的脐橙是“特级果”,有一果农今年种植脐橙,大获丰收为了了解脐橙的品质,随机摘取100个脐橙进行检测,其重量分别在[0.1,0.2),[0.2,0.3),[0.3,0.4),[0.4,0.5),[0.5,0.6),[0.6,0.7]中,经统计得到如图所示频率分布直方图
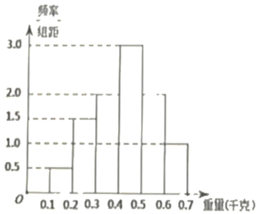
(1)将频率视为概率,用样本估计总体.现有一名消费者从脐橙果园中,随机摘取5个脐橙,求恰有3个是“精品果”的概率.
(2)现从摘取的100个脐橙中,采用分层抽样的方式从重量为[0.4,0.5),[0.5,0.6)的脐橙中随机抽取10个,再从这10个抽取3个,记随机变量X表示重量在[0.5,0.6)内的脐橙个数,求X的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】条形码![]() 是将宽度不等的多个黑条和空白,按照一定的编码规则排列,用以表达一组信息的图形标识符。常见的条形码是“
是将宽度不等的多个黑条和空白,按照一定的编码规则排列,用以表达一组信息的图形标识符。常见的条形码是“![]() ”通用代码,它是由从左到右排列的13个数字(用
”通用代码,它是由从左到右排列的13个数字(用![]() 表示)组成,其中
表示)组成,其中![]() 是校验码,用来校验前12个数字代码的正确性.下面的框图是计算第13位校验码的程序框图,框图中符号
是校验码,用来校验前12个数字代码的正确性.下面的框图是计算第13位校验码的程序框图,框图中符号![]() 表示不超过
表示不超过![]() 的最大整数(例如
的最大整数(例如![]() ).现有一条形码如图(1)所示
).现有一条形码如图(1)所示![]() ,其中第6个数被污损, 那么这个被污损数字
,其中第6个数被污损, 那么这个被污损数字![]() 是( )
是( )


A. 6 B. 7 C. 8 D. 9
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=2x-1,![]() (a∈R),若对任意x1∈[1,+∞),总存在x2∈R,使f(x1)=g(x2),则实数a的取值范围是()
(a∈R),若对任意x1∈[1,+∞),总存在x2∈R,使f(x1)=g(x2),则实数a的取值范围是()
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为回馈顾客,新华都购物商场拟通过摸球兑奖的方式对500位顾客进行奖励,规定:每位顾客从一个装有4个标有面值的球的袋中一次性随机摸出2个球(球的大小、形状一模一样),球上所标的面值之和为该顾客所获的奖励额.
(1)若袋中所装的4个球中有1个所标的面值为40元,其余3个所标的面值均为20元,求顾客所获的奖励额![]() 的分布列及数学期望;
的分布列及数学期望;
(2)商场对奖励总额的预算是30000元,并规定袋中的4个球由标有面值为20元和40元的两种球共同组成,或标有面值为15元和45元的两种球共同组成.为了使顾客得到的奖励总额尽可能符合商场的预算且每位顾客所获的奖励额相对均衡.请对袋中的4个球的面值给出一个合适的设计,并说明理由.
提示:袋中的4个球由标有面值为a元和b元的两种球共同组成,即袋中的4个球所标的面值“既有a元又有b元”.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com