
分析 由条件便可得到$λ=cos<\overrightarrow{OA},\overrightarrow{OM}>$,从而求向量$\overrightarrow{OA},\overrightarrow{OM}$的夹角的范围便可得出λ的范围,可以找出平面区域D,结合图形即可找出向量$\overrightarrow{OA},\overrightarrow{OM}$的范围,从而得出$cos<\overrightarrow{OA},\overrightarrow{OM}>$的范围,即得出λ的取值范围.
解答 解:根据条件,$|\overrightarrow{OA}|=1$,$\overrightarrow{OA}•\overrightarrow{OM}=|\overrightarrow{OA}||\overrightarrow{OM}|cos<\overrightarrow{OA},\overrightarrow{OM}>$=$|\overrightarrow{OM}|cos<\overrightarrow{OA},\overrightarrow{OM}>=λ|\overrightarrow{OM}|$;
∴$λ=cos<\overrightarrow{OA},\overrightarrow{OM}>$;
由$\left\{\begin{array}{l}{8x-4≥0}\\{(y-1)(3x+y-6)≤0}\end{array}\right.$得,$\left\{\begin{array}{l}{8x-4≥0}\\{y-1≥0}\\{3x+y-6≤0}\end{array}\right.$,或$\left\{\begin{array}{l}{8x-4≥0}\\{y-1≤0}\\{3x+y-6≥0}\end{array}\right.$;
∴平面区域D如下图所示: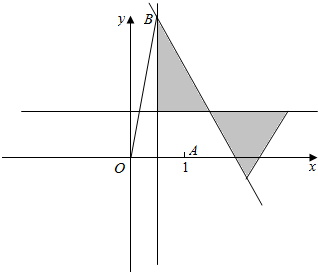
设直线8x-4=0和直线3x+y-6=0的交点为B($\frac{1}{2},\frac{9}{2}$);
设OB的倾斜角为θ1,直线3x+y-6=0的倾斜角为θ2,则向量$\overrightarrow{OA},\overrightarrow{OM}$夹角的范围为[0,θ1]∪(θ2,π];
$cos{θ}_{1}=\frac{\frac{1}{2}}{\sqrt{\frac{1}{4}+\frac{81}{4}}}=\frac{\sqrt{82}}{82}$,tanθ2=-3,∴$cos{θ}_{2}=-\frac{\sqrt{10}}{10}$;
∴$cos<\overrightarrow{OA},\overrightarrow{OM}>$$∈[\frac{\sqrt{82}}{82},1]∪[-1,-\frac{\sqrt{10}}{10})$;
∴λ的取值范围为[$\frac{\sqrt{82}}{82},1$]∪[-1,$-\frac{\sqrt{10}}{10}$).
故答案为:[$\frac{\sqrt{82}}{82},1$]∪[-1,$-\frac{\sqrt{10}}{10}$).
点评 考查线性规划的知识,能找出不等式组所表示的平面区域,向量数量积的计算公式,向量夹角的概念,以及数形结合解题的方法.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
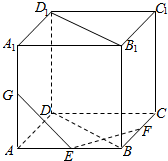 如图,在棱长为2的正方体ABCD一A1B1C1D1中,点E,F,G分别是边AB,BC,AA1上的点,记AE=x,BF=y,A1G=z,
如图,在棱长为2的正方体ABCD一A1B1C1D1中,点E,F,G分别是边AB,BC,AA1上的点,记AE=x,BF=y,A1G=z,查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com