
分析 (Ⅰ)根据题目中的数据用茎叶图表示即可;
(Ⅱ)计算甲、乙的平均数与方差,比较即可得出结论.
解答 解:(Ⅰ)题目中的数据用茎叶图表示如下:…(3分)
(Ⅱ)计算甲的平均数为$\overline{{x}_{1}}$=$\frac{1}{5}$×(74+76+78+82+90)=80,
乙的平均数为$\overline{{x}_{2}}$=$\frac{1}{5}$×(70+75+80+85+90)=80,…(7分)
而甲的方差为${{s}_{1}}^{2}$=$\frac{1}{5}$×[(78-80)2+(76-80)2+(74-80)2+(90-80)2+(82-80)2]=32,
乙的方差为${{s}_{2}}^{2}$=$\frac{1}{5}$×[(90-80)2+(70-80)2+(75-80)2+(85-80)2+(80-80)2]=50,…(11分)
因为$\overline{{x}_{1}}$=$\overline{{x}_{2}}$,${{s}_{1}}^{2}$<${{s}_{2}}^{2}$,
所以在平均数一样的条件下,甲的水平更为稳定,应该派甲去.…(12分)
点评 本题考查了茎叶图以及平均数与方差的应用问题,是基础题目.


 小学课时特训系列答案
小学课时特训系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
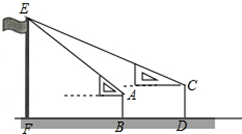 某校高一年级某班开展数学活动,小李和小军合作用一副三角板测量学校的旗杆,小李站在B点测得旗杆顶端E点的仰角为45°,小军站在点D测得旗杆顶端E点的仰角为30°,已知小李和小军相距(BD)6米,小李的身高(AB)1.5米,小军的身高(CD)1.75米,求旗杆的高EF的长.(结果精确到0.1,参考数据:$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73)
某校高一年级某班开展数学活动,小李和小军合作用一副三角板测量学校的旗杆,小李站在B点测得旗杆顶端E点的仰角为45°,小军站在点D测得旗杆顶端E点的仰角为30°,已知小李和小军相距(BD)6米,小李的身高(AB)1.5米,小军的身高(CD)1.75米,求旗杆的高EF的长.(结果精确到0.1,参考数据:$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73)查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ($\frac{3}{2}$,+∞) | B. | (-∞,-$\frac{3}{2}$) | C. | (-∞,-$\frac{3}{2}$)∪($\frac{3}{2}$,+∞) | D. | (-$\frac{3}{2}$,$\frac{3}{2}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-$\frac{2π}{3}$,$\frac{π}{3}$] | B. | [$\frac{π}{3}$,$\frac{4π}{3}$] | C. | [-$\frac{5π}{3}$,-$\frac{2π}{3}$] | D. | [0,π] |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com