
【题目】下列不等式中解集为实数集R的是( )
A.x2+4x+4>0
B.![]()
C.x2﹣x+1≥0
D.![]()
【答案】C
【解析】解:A、x2+4x+4>0变形为:(x+2)2>0,
∴不等式的解集为x≠﹣2,不合题意;
B、 ![]() >0,则x是不为0的实数,不合题意;
>0,则x是不为0的实数,不合题意;
C、x2﹣x+1≥0,
令x2﹣x+1=0,∵a=1,b=﹣1,c=1,∴b2﹣4ac=﹣3<0,
∴x2﹣x+1=0无解,
则x2﹣x+1≥0解集为R,符合题意;
D、 ![]() ,当x≠0时,去分母得:﹣1<0,恒成立,
,当x≠0时,去分母得:﹣1<0,恒成立,
则不等式的解集为x≠0,不合题意,
故选C
【考点精析】解答此题的关键在于理解解一元二次不等式的相关知识,掌握求一元二次不等式![]()
![]() 解集的步骤:一化:化二次项前的系数为正数;二判:判断对应方程的根;三求:求对应方程的根;四画:画出对应函数的图象;五解集:根据图象写出不等式的解集;规律:当二次项系数为正时,小于取中间,大于取两边.
解集的步骤:一化:化二次项前的系数为正数;二判:判断对应方程的根;三求:求对应方程的根;四画:画出对应函数的图象;五解集:根据图象写出不等式的解集;规律:当二次项系数为正时,小于取中间,大于取两边.


 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案科目:高中数学 来源: 题型:
【题目】(本小题满分为16分)设A,B分别为椭圆![]()
![]() 的左、右顶点,椭圆的长轴长为
的左、右顶点,椭圆的长轴长为![]() ,且点
,且点![]() 在该椭圆上.
在该椭圆上.
(1)求椭圆的方程;
(2)设![]() 为直线
为直线![]() 上不同于点
上不同于点![]() 的任意一点,若直线
的任意一点,若直线![]() 与椭圆相交于异于
与椭圆相交于异于![]() 的点
的点![]() ,证明:△
,证明:△![]() 为钝角三角形.
为钝角三角形.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分10分)设![]() 个正数
个正数![]() 满足
满足![]() (
(![]() 且
且![]() ).
).
(1)当![]() 时,证明:
时,证明:![]() ;
;
(2)当![]() 时,不等式
时,不等式![]() 也成立,请你将其推广到
也成立,请你将其推广到![]() (
(![]() 且
且![]() )个正数
)个正数![]() 的情形,归纳出一般性的结论并用数学归纳法证明.
的情形,归纳出一般性的结论并用数学归纳法证明.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在底面是正方形的四棱锥P﹣ABCD中,PA⊥面ABCD,BD交AC于点E,F是PC中点,G为AC上一点. 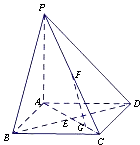
(1)求证:BD⊥FG;
(2)确定点G在线段AC上的位置,使FG∥平面PBD,并说明理由;
(3)当二面角B﹣PC﹣D的大小为 ![]() 时,求PC与底面ABCD所成角的正切值.
时,求PC与底面ABCD所成角的正切值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知向量 ![]() =(cos2x,
=(cos2x, ![]() sinx),
sinx), ![]() =(1,cosx),函数f(x)=2
=(1,cosx),函数f(x)=2 ![]()
![]() +m,且当x∈[0,
+m,且当x∈[0, ![]() ]时,f(x)的最小值为2.
]时,f(x)的最小值为2.
(1)求m的值,并求f(x)图象的对称轴方程;
(2)设函数g(x)=[f(x)2]﹣f(x),x∈[0, ![]() ],求g(x)的最大值.
],求g(x)的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂利用随机数表对生产的700个零件进行抽样测试,先将700个零件进行编号001,002,…,699,700.从中抽取70个样本,如图提供随机数表的第4行到第6行,若从表中第5行第6列开始向右读取数据,则得到的第5个样本编号是( ) 
A.607
B.328
C.253
D.007
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知椭圆![]() ,点B是其下顶点,过点B的直线交椭圆C于另一点A(A点在
,点B是其下顶点,过点B的直线交椭圆C于另一点A(A点在![]() 轴下方),且线段AB的中点E在直线
轴下方),且线段AB的中点E在直线![]() 上.
上.
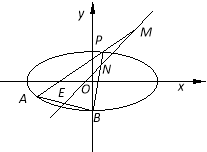
(1)求直线AB的方程;
(2)若点P为椭圆C上异于A、B的动点,且直线AP,BP分别交直线![]() 于点M、N,证明:OM·ON为定值.
于点M、N,证明:OM·ON为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图是我国南宋时期的数学家秦九韶提出的一种多项式f(x)=anxn+an﹣1xn﹣1+…+a1x+a0的求值问题的算法.现按照这个程序执行函数f (x)=3x4﹣2x3﹣6x﹣17的计算,若输入的值x0=2,则输出的v的值是( ) 
A.0
B.2
C.3
D.﹣3
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com