
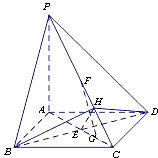
【题目】如图,在底面是正方形的四棱锥P﹣ABCD中,PA⊥面ABCD,BD交AC于点E,F是PC中点,G为AC上一点. 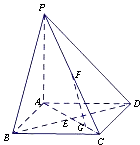
(1)求证:BD⊥FG;
(2)确定点G在线段AC上的位置,使FG∥平面PBD,并说明理由;
(3)当二面角B﹣PC﹣D的大小为 ![]() 时,求PC与底面ABCD所成角的正切值.
时,求PC与底面ABCD所成角的正切值.
【答案】
(1)证明:∵PA⊥面ABCD,四边形ABCD是正方形,其对角线BD,AC交于点E,
∴PA⊥BD,AC⊥BD,
∴BD⊥平面PAC,
∵FG平面PAC,
∴BD⊥FG
或用向量方法:
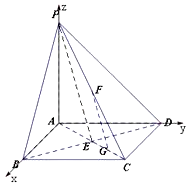
解:以A为原点,AB,AD,AP所在的直线分别为x,y,z轴建立空间直角坐标系如图所示,设正方形ABCD的边长为1,则A(0,0,0),B(1,0,0),C(1,1,0),D(0,1,0),P(0,0,a)(a>0),
E( ![]() ),F(
),F( ![]() ),G(m,m,0)(0<m<
),G(m,m,0)(0<m< ![]() )
)
![]() =(﹣1,1,0),
=(﹣1,1,0), ![]() =(
=( ![]() ),
), ![]() ×
× ![]() =﹣m+
=﹣m+ ![]() +m﹣
+m﹣ ![]() +0=0,
+0=0,
∴BD⊥FG
(2)解:当G为EC中点,即AG= ![]() AC时,FG∥平面PBD,
AC时,FG∥平面PBD,
理由如下:
连接PE,由F为PC中点,G为EC中点,知FG∥PE,
而FG平面PBD,PE平面PBD,
故FG∥平面PBD.
或用向量方法:
要使FG∥平面PBD,只需FG∥EP,而 ![]() =(
=( ![]() ),由
),由 ![]() =
= ![]()
![]() 可得
可得 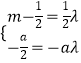 ,
,
解得l=1,m= ![]() ,
,
∴G( ![]() ,
, ![]() ,0),∴
,0),∴ ![]() ,
,
故当AG= ![]() AC时,FG∥平面PBD
AC时,FG∥平面PBD
(3)解:作BH⊥PC于H,连接DH,
∵PA⊥面ABCD,四边形ABCD是正方形,
∴PB=PD,
又∵BC=DC,PC=PC,
∴△PCB≌△PCD,
∴DH⊥PC,且DH=BH,
∴∠BHD就是二面角B﹣PC﹣D的平面角,
即∠BHD= ![]() ,
,
∵PA⊥面ABCD,∴∠PCA就是PC与底面ABCD所成的角
连接EH,则EH⊥BD,∠BHE= ![]() ,EH⊥PC,
,EH⊥PC,
∴tan∠BHE= ![]() ,而BE=EC,
,而BE=EC,
∴ ![]() ,∴sin∠PCA=
,∴sin∠PCA= ![]() ,∴tan∠PCA=
,∴tan∠PCA= ![]() ,
,
∴PC与底面ABCD所成角的正切值是 ![]()
或用向量方法:
设平面PBC的一个法向量为 ![]() =(x,y,z),
=(x,y,z),
则 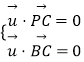 ,而
,而 ![]() ,
, ![]() ,
,
∴ ![]() ,取z=1,得
,取z=1,得 ![]() =(a,0,1),同理可得平面PDC的一个法向量为
=(a,0,1),同理可得平面PDC的一个法向量为 ![]() =(0,a,1),
=(0,a,1),
设 ![]() ,
, ![]() 所成的角为β,则|cosβ|=|cos
所成的角为β,则|cosβ|=|cos ![]() |=
|= ![]() ,即
,即 ![]() =
= ![]() ,∴
,∴ ![]() ,∴a=1
,∴a=1
∵PA⊥面ABCD,∴∠PCA就是PC与底面ABCD所成的角,
∴tan∠PCA= ![]()
【解析】(1)要证:BD⊥FG,先证BD⊥平面PAC即可.(2)确定点G在线段AC上的位置,使FG∥平面PBD,FG∥平面PBD内的一条直线即可.(3)当二面角B﹣PC﹣D的大小为 ![]() 时,求PC与底面ABCD所成角的正切值.只要作出二面角的平面角,解三角形即可求出结果.这三个问题可以利用空间直角坐标系,解答(1)求数量积即可.(2)设才点的坐标,向量共线即可解答.(3)利用向量数量积求解法向量,然后转化求出PC与底面ABCD所成角的正切值.
时,求PC与底面ABCD所成角的正切值.只要作出二面角的平面角,解三角形即可求出结果.这三个问题可以利用空间直角坐标系,解答(1)求数量积即可.(2)设才点的坐标,向量共线即可解答.(3)利用向量数量积求解法向量,然后转化求出PC与底面ABCD所成角的正切值.
【考点精析】通过灵活运用空间中直线与直线之间的位置关系和平面与平面之间的位置关系,掌握相交直线:同一平面内,有且只有一个公共点;平行直线:同一平面内,没有公共点;异面直线: 不同在任何一个平面内,没有公共点;两个平面平行没有交点;两个平面相交有一条公共直线即可以解答此题.


科目:高中数学 来源: 题型:
【题目】(本小题满分16分)
在平面直角坐标系xOy中,椭圆C:![]() (a>b>0)的上顶点到焦点的距离为2,离心率为
(a>b>0)的上顶点到焦点的距离为2,离心率为![]() .
.
(1)求a,b的值.
(2)设P是椭圆C长轴上的一个动点,过点P作斜率为k的直线l交椭圆C于A、B两点.
(ⅰ)若k=1,求△OAB面积的最大值;
(ⅱ)若PA2+PB2的值与点P的位置无关,求k的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() ﹣2ax+1+lnx
﹣2ax+1+lnx
(1)当a=0时,若函数f(x)在其图象上任意一点A处的切线斜率为k,求k的最小值,并求此时的切线方程;
(2)若函数f(x)的极大值点为x1 , 证明:x1lnx1﹣ax12>﹣1.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分16分)在平面直角坐标系![]() 中,已知椭圆
中,已知椭圆![]() :
: ![]() 的离心率
的离心率![]() ,直线
,直线![]() 过椭圆
过椭圆![]() 的右焦点
的右焦点![]() ,且交椭圆
,且交椭圆![]() 于
于![]() ,
, ![]() 两点.
两点.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)已知点![]() ,连结
,连结![]() ,过点
,过点![]() 作垂直于
作垂直于![]() 轴的直线
轴的直线![]() ,设直线
,设直线![]() 与直线
与直线![]() 交于点
交于点![]() ,试探索当
,试探索当![]() 变化时,是否存在一条定直线
变化时,是否存在一条定直线![]() ,使得点
,使得点![]() 恒在直线
恒在直线![]() 上?若存在,请求出直线
上?若存在,请求出直线![]() 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分10分)一位网民在网上光顾某淘宝小店,经过一番浏览后,对该店铺中的![]() 五种商品有购买意向.已知该网民购买
五种商品有购买意向.已知该网民购买![]() 两种商品的概率均为
两种商品的概率均为![]() ,购买
,购买![]() 两种商品的概率均为
两种商品的概率均为![]() ,购买
,购买![]() 种商品的概率为
种商品的概率为![]() .假设该网民是否购买这五种商品相互独立.
.假设该网民是否购买这五种商品相互独立.
(1)求该网民至少购买4种商品的概率;
(2)用随机变量![]() 表示该网民购买商品的种数,求
表示该网民购买商品的种数,求![]() 的概率分布和数学期望.
的概率分布和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,角A、B、C的对边分别为a,b,c,且满足(2a﹣c)cosB=bcosC
(1)求角B的大小;
(2)若b= ![]() ,a+c=4,求△ABC的面积S.
,a+c=4,求△ABC的面积S.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,其中
,其中![]() 为自然对数底数.
为自然对数底数.
(1)当![]() 时,求函数
时,求函数![]() 在点
在点![]() 处的切线方程;
处的切线方程;
(2)讨论函数![]() 的单调性,并写出相应的单调区间;
的单调性,并写出相应的单调区间;
(3)已知![]() ,若函数
,若函数![]() 对任意
对任意![]() 都成立,求
都成立,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若![]() 是两个相交平面,则在下列命题中,真命题的序号为 .(写出所有真命题的序号)
是两个相交平面,则在下列命题中,真命题的序号为 .(写出所有真命题的序号)
①若直线![]() ,则在平面
,则在平面![]() 内,一定不存在与直线
内,一定不存在与直线![]() 平行的直线.
平行的直线.
②若直线![]() ,则在平面
,则在平面![]() 内,一定存在无数条直线与直线
内,一定存在无数条直线与直线![]() 垂直.
垂直.
③若直线![]() ,则在平面
,则在平面![]() 内,不一定存在与直线
内,不一定存在与直线![]() 垂直的直线.
垂直的直线.
④若直线![]() ,则在平面
,则在平面![]() 内,一定存在与直线
内,一定存在与直线![]() 垂直的直线.
垂直的直线.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com