
【题目】在△ABC中,角A、B、C的对边分别为a,b,c,且满足(2a﹣c)cosB=bcosC
(1)求角B的大小;
(2)若b= ![]() ,a+c=4,求△ABC的面积S.
,a+c=4,求△ABC的面积S.
【答案】
(1)解:在△ABC中,由(2a﹣c)cosB=bcosC以及正弦定理可得
2sinAcosB﹣sinCcosB=sinBcosC,即 2sinAcosB=sin(B+C)=sinA,
求得cosB= ![]() ,可得 B=
,可得 B= ![]()
(2)解:若 ![]() ,由余弦定理可得 cosB=
,由余弦定理可得 cosB= ![]() =
= ![]() =
= ![]() =
= ![]() ,
,
故有ac=3,
故△ABC的面积S= ![]() acsinB=
acsinB= ![]() ×3×sin
×3×sin ![]() =
= ![]()
【解析】(1)在△ABC中,由(2a﹣c)cosB=bcosC以及正弦定理可得2sinAcosB=sin(B+C)=sinA,求得cosB的值,
可得 B的值.(2)由条件利用余弦定理可得 cosB= ![]() =
= ![]() ,可得ac=3,从而求得△ABC的面积S=
,可得ac=3,从而求得△ABC的面积S= ![]() acsinB 的值.
acsinB 的值.
【考点精析】本题主要考查了正弦定理的定义和余弦定理的定义的相关知识点,需要掌握正弦定理:![]() ;余弦定理:
;余弦定理:![]() ;
;![]() ;
;![]() 才能正确解答此题.
才能正确解答此题.


科目:高中数学 来源: 题型:
【题目】如图所示,正方形AA1D1D与矩形ABCD所在平面互相垂直,AB=2AD=2,点E为AB的中点. 
(1)求证:BD1∥平面A1DE;
(2)求直线A1E与平面AD1E所成角.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知F为抛物线y2=x的焦点,点A,B在该抛物线上且位于x轴的两侧, ![]() =2(其中O为坐标原点),则△ABO与△AFO面积之和的最小值是( )
=2(其中O为坐标原点),则△ABO与△AFO面积之和的最小值是( )
A.2
B.3
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在底面是正方形的四棱锥P﹣ABCD中,PA⊥面ABCD,BD交AC于点E,F是PC中点,G为AC上一点. 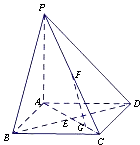
(1)求证:BD⊥FG;
(2)确定点G在线段AC上的位置,使FG∥平面PBD,并说明理由;
(3)当二面角B﹣PC﹣D的大小为 ![]() 时,求PC与底面ABCD所成角的正切值.
时,求PC与底面ABCD所成角的正切值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下面有五个命题:
①函数y=sin4x﹣cos4x的最小正周期是π;
② ![]() =tanα;
=tanα;
③函数y=sinx+cosx的图象均关于点( ![]() ,0)成中心对称;
,0)成中心对称;
④把函数y=3sin(2x+ ![]() )的图象向右平移
)的图象向右平移 ![]() 个单位得到y=3sin2x的图象.
个单位得到y=3sin2x的图象.
其中正确命题的编号是 . (写出所有正确命题的编号)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂利用随机数表对生产的700个零件进行抽样测试,先将700个零件进行编号001,002,…,699,700.从中抽取70个样本,如图提供随机数表的第4行到第6行,若从表中第5行第6列开始向右读取数据,则得到的第5个样本编号是( ) 
A.607
B.328
C.253
D.007
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=sin(ωx+φ)(ω>0,|φ|< ![]() )的最小正周期是π,若将其图象向右平移
)的最小正周期是π,若将其图象向右平移 ![]() 个单位后得到的图象关于原点对称,则函数f(x)的图象( )
个单位后得到的图象关于原点对称,则函数f(x)的图象( )
A.关于直线x= ![]() 对称
对称
B.关于直线x= ![]() 对称
对称
C.关于点( ![]() ,0)对称
,0)对称
D.关于点( ![]() ,0)对称
,0)对称
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本题满分16分)数列![]() ,
, ![]() ,
, ![]() 满足:
满足: ![]() ,
, ![]() ,
, ![]() .
.
(1)若数列![]() 是等差数列,求证:数列
是等差数列,求证:数列![]() 是等差数列;
是等差数列;
(2)若数列![]() ,
, ![]() 都是等差数列,求证:数列
都是等差数列,求证:数列![]() 从第二项起为等差数列;
从第二项起为等差数列;
(3)若数列![]() 是等差数列,试判断当
是等差数列,试判断当![]() 时,数列
时,数列![]() 是否成等差数列?证明你的结论.
是否成等差数列?证明你的结论.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在半径为 ![]() ,圆心角为60°的扇形的弧上任取一点P,作扇形的内接矩形PNMQ,使点Q在OA上,点N,M在OB上,设矩形PNMQ的面积为y,∠POB=θ.
,圆心角为60°的扇形的弧上任取一点P,作扇形的内接矩形PNMQ,使点Q在OA上,点N,M在OB上,设矩形PNMQ的面积为y,∠POB=θ. 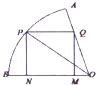
(1)将y表示成θ的函数关系式,并写出定义域;
(2)求矩形PNMQ的面积取得最大值时 ![]()
![]() 的值;
的值;
(3)求矩形PNMQ的面积y≥ ![]() 的概率.
的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com