
【题目】如图,在半径为 ![]() ,圆心角为60°的扇形的弧上任取一点P,作扇形的内接矩形PNMQ,使点Q在OA上,点N,M在OB上,设矩形PNMQ的面积为y,∠POB=θ.
,圆心角为60°的扇形的弧上任取一点P,作扇形的内接矩形PNMQ,使点Q在OA上,点N,M在OB上,设矩形PNMQ的面积为y,∠POB=θ. 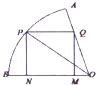
(1)将y表示成θ的函数关系式,并写出定义域;
(2)求矩形PNMQ的面积取得最大值时 ![]()
![]() 的值;
的值;
(3)求矩形PNMQ的面积y≥ ![]() 的概率.
的概率.
【答案】
(1)解:在Rt△PON中,∠PNO=90°,∠POB=θ, ![]() ,
,
所以 ![]() ,
, ![]() ,
,
在Rt△QMO中,∠QMO=90°,∠QON=60°,QM=PN= ![]()
所以OM= ![]()
所以:MN=ON﹣OM= ![]()
所以y= ![]()
即:y=3sinθcosθ﹣ ![]() sin2θ,(
sin2θ,( ![]() )
)
(2)解:由(1)得y=3sinθcosθ﹣ ![]() sin2θ=
sin2θ= ![]() ﹣
﹣ ![]()
= ![]() )﹣
)﹣ ![]() =
= ![]()
∵θ∈(0, ![]() )
)
∴ ![]()
∴sin( ![]() )∈
)∈ ![]()
∴ ![]() ,即
,即 ![]() 时,y的最大值为
时,y的最大值为 ![]() .
.
此时ON= ![]() cos
cos ![]() =
= ![]() =
= ![]() ,则
,则 ![]()
![]() =|
=| ![]() ||
|| ![]() |cos
|cos ![]() =
= ![]() ×
× ![]() =
= ![]() .
.
(3)解:若矩形PNMQ的面积y≥ ![]() ,
,
则 ![]() ≥
≥ ![]() ,
,
即 ![]() sin(
sin( ![]() )≥
)≥ ![]() ,
,
则sin( ![]() )≥
)≥ ![]() ,
,
∵ ![]()
∴ ![]() ≤
≤ ![]() ≤
≤ ![]() ,
,
即 ![]() ≤θ≤
≤θ≤ ![]() ,
,
则对应的概率P= ![]() =
= ![]()
【解析】(1)利用三角函数的关系,求出矩形的邻边,求出面积的表达式,化为一个角的一个三角函数的形式,根据θ的范围确定函数的定义域.(2)利用三角函数的倍角公式以及辅助角公式将函数进行化简,结合三角函数的最值性质求出矩形面积的最大值.以及利用向量数量积的定义进行求解即可.(3)根据几何概型的概率公式求出矩形PNMQ的面积y≥ ![]() 时,对应的角θ的取值范围,即可得到结论.
时,对应的角θ的取值范围,即可得到结论.
【考点精析】本题主要考查了几何概型的相关知识点,需要掌握几何概型的特点:1)试验中所有可能出现的结果(基本事件)有无限多个;2)每个基本事件出现的可能性相等才能正确解答此题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】在△ABC中,角A、B、C的对边分别为a,b,c,且满足(2a﹣c)cosB=bcosC
(1)求角B的大小;
(2)若b= ![]() ,a+c=4,求△ABC的面积S.
,a+c=4,求△ABC的面积S.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角△ABC中,∠BCA=90°,CA=CB=1,P为AB边上的点且 ![]() =λ
=λ ![]() ,若
,若 ![]()
![]() ≥
≥ ![]()
![]() ,则λ的取值范围是( )
,则λ的取值范围是( )
A.[ ![]() ,1]
,1]
B.[ ![]() ,1]
,1]
C.[ ![]() ,
, ![]() ]
]
D.[ ![]() ,
, ![]() ]
]
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若![]() 是两个相交平面,则在下列命题中,真命题的序号为 .(写出所有真命题的序号)
是两个相交平面,则在下列命题中,真命题的序号为 .(写出所有真命题的序号)
①若直线![]() ,则在平面
,则在平面![]() 内,一定不存在与直线
内,一定不存在与直线![]() 平行的直线.
平行的直线.
②若直线![]() ,则在平面
,则在平面![]() 内,一定存在无数条直线与直线
内,一定存在无数条直线与直线![]() 垂直.
垂直.
③若直线![]() ,则在平面
,则在平面![]() 内,不一定存在与直线
内,不一定存在与直线![]() 垂直的直线.
垂直的直线.
④若直线![]() ,则在平面
,则在平面![]() 内,一定存在与直线
内,一定存在与直线![]() 垂直的直线.
垂直的直线.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系中,曲线C1的参数方程为: ![]() (α为参数),以原点为极点,x轴的正半轴为极轴,并取与直角坐标系相同的长度单位,建立极坐标系,曲线C2的极坐标方程为:ρ=cosθ. (Ⅰ)求曲线C2的直角坐标方程;
(α为参数),以原点为极点,x轴的正半轴为极轴,并取与直角坐标系相同的长度单位,建立极坐标系,曲线C2的极坐标方程为:ρ=cosθ. (Ⅰ)求曲线C2的直角坐标方程;
(Ⅱ)若P,Q分别是曲线C1和C2上的任意一点,求|PQ|的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)在R上可导,其导函数为f′(x),且函数y=(1﹣x)f′(x)的图像如图所示,则下列结论中一定成立的是( ) 
A.函数f(x)有极大值f(2)和极小值f(1)
B.函数f(x)有极大值f(﹣2)和极小值f(1)
C.函数f(x)有极大值f(2)和极小值f(﹣2)
D.函数f(x)有极大值f(﹣2)和极小值f(2)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)= ![]() x2+ax﹣lnx(a∈R).
x2+ax﹣lnx(a∈R).
(1)当a=1时,求函数f(x)的极值;
(2)当a>1时,讨论函数f(x)的单调性;
(3)若对任意a∈(3,4)及任意x1 , x2∈[1,2],恒有 ![]() m+ln2>|f(x1)﹣f(x2)|成立,求实数m的取值范围.
m+ln2>|f(x1)﹣f(x2)|成立,求实数m的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com