
【题目】在直角△ABC中,∠BCA=90°,CA=CB=1,P为AB边上的点且 ![]() =λ
=λ ![]() ,若
,若 ![]()
![]() ≥
≥ ![]()
![]() ,则λ的取值范围是( )
,则λ的取值范围是( )
A.[ ![]() ,1]
,1]
B.[ ![]() ,1]
,1]
C.[ ![]() ,
, ![]() ]
]
D.[ ![]() ,
, ![]() ]
]
科目:高中数学 来源: 题型:
【题目】已知F为抛物线y2=x的焦点,点A,B在该抛物线上且位于x轴的两侧, ![]() =2(其中O为坐标原点),则△ABO与△AFO面积之和的最小值是( )
=2(其中O为坐标原点),则△ABO与△AFO面积之和的最小值是( )
A.2
B.3
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=sin(ωx+φ)(ω>0,|φ|< ![]() )的最小正周期是π,若将其图象向右平移
)的最小正周期是π,若将其图象向右平移 ![]() 个单位后得到的图象关于原点对称,则函数f(x)的图象( )
个单位后得到的图象关于原点对称,则函数f(x)的图象( )
A.关于直线x= ![]() 对称
对称
B.关于直线x= ![]() 对称
对称
C.关于点( ![]() ,0)对称
,0)对称
D.关于点( ![]() ,0)对称
,0)对称
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本题满分16分)数列![]() ,
, ![]() ,
, ![]() 满足:
满足: ![]() ,
, ![]() ,
, ![]() .
.
(1)若数列![]() 是等差数列,求证:数列
是等差数列,求证:数列![]() 是等差数列;
是等差数列;
(2)若数列![]() ,
, ![]() 都是等差数列,求证:数列
都是等差数列,求证:数列![]() 从第二项起为等差数列;
从第二项起为等差数列;
(3)若数列![]() 是等差数列,试判断当
是等差数列,试判断当![]() 时,数列
时,数列![]() 是否成等差数列?证明你的结论.
是否成等差数列?证明你的结论.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,已知角A、B、C所对的边分别为a、b、c,且a2+b2﹣c2= ![]() ab.
ab. 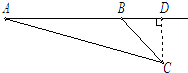
(1)求角C的大小;
(2)如果0<A≤ ![]() ,m=2cos2
,m=2cos2 ![]() ﹣sinB﹣1,求实数m的取值范围.
﹣sinB﹣1,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ln(x+ ![]() ﹣2)(a>0) (Ⅰ)当1<a<4时,函数f(x)在[2,4]上的最小值为ln
﹣2)(a>0) (Ⅰ)当1<a<4时,函数f(x)在[2,4]上的最小值为ln ![]() ,求a;
,求a;
(Ⅱ)若存在x0∈(2,+∞),使得f(x0)<0,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在半径为 ![]() ,圆心角为60°的扇形的弧上任取一点P,作扇形的内接矩形PNMQ,使点Q在OA上,点N,M在OB上,设矩形PNMQ的面积为y,∠POB=θ.
,圆心角为60°的扇形的弧上任取一点P,作扇形的内接矩形PNMQ,使点Q在OA上,点N,M在OB上,设矩形PNMQ的面积为y,∠POB=θ. 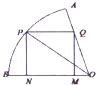
(1)将y表示成θ的函数关系式,并写出定义域;
(2)求矩形PNMQ的面积取得最大值时 ![]()
![]() 的值;
的值;
(3)求矩形PNMQ的面积y≥ ![]() 的概率.
的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某海滨浴场每年夏季每天的海浪高度y(米)是时间x(0≤x≤24,单位:小时)的函数,记作y=f(x),下表是每年夏季每天某些时刻的浪高数据:
x(时) | 0 | 3 | 6 | 9 | 12 | 15 | 18 | 21 | 24 |
y(米) | 1.5 | 1.0 | 0.5 | 1.0 | 1.5 | 1.0 | 0.5 | 1.0 | 1.5 |
(1)经观察发现可以用三角函数y=Acosωx+b对这些数据进行拟合,求函数f(x)的表达式;
(2)浴场规定,每天白天当海浪高度高于1.25米时,才对冲浪爱好者开放,求冲浪者每天白天可以在哪个时段到该浴场进行冲浪运动?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com