
【题目】已知函数f(x)= ![]() ﹣2ax+1+lnx
﹣2ax+1+lnx
(1)当a=0时,若函数f(x)在其图象上任意一点A处的切线斜率为k,求k的最小值,并求此时的切线方程;
(2)若函数f(x)的极大值点为x1 , 证明:x1lnx1﹣ax12>﹣1.
【答案】
(1)解:∵a=0,∴ ![]() ,
,
∴ ![]() ,当仅当
,当仅当 ![]() 时,即x=1时,f'(x)的最小值为2,
时,即x=1时,f'(x)的最小值为2,
∴斜率k的最小值为2,切点A ![]() ,
,
∴切线方程为 ![]() ,即4x﹣2y﹣1=0;
,即4x﹣2y﹣1=0;
(2)解:∵ ![]() ,
,
①当﹣1≤a≤1时,f(x)单调递增无极值点,不符合题意;
②当a>1或a<﹣1时,令f'(x)=0,设x2﹣2ax+1=0的两根为x1和x2,
因为x1为函数f(x)的极大值点,所以0<x1<x2,
又x1x2=1,x1+x2=2a>0,∴a>1,0<x1<1,
∴f′(x1)=0, ![]() ,则
,则 ![]() ,
,
∵ ![]() =
= ![]() =
= ![]() ,x1∈(0,1),
,x1∈(0,1),
令 ![]() ,x∈(0,1),
,x∈(0,1),
∴ ![]() ,∴h′(x)=﹣3x+
,∴h′(x)=﹣3x+ ![]() =
= ![]() ,x∈(0,1),
,x∈(0,1),
当 ![]() 时,h′(x)>0,当
时,h′(x)>0,当 ![]() 时,h′(x)<0,
时,h′(x)<0,
∴h′(x)在 ![]() 上单调递增,在
上单调递增,在 ![]() 上单调递减,
上单调递减,
∴ ![]() ,
,
∴h(x)在(0,1)上单调递减.
∴h(x)>h(1)=﹣1,原题得证.
【解析】(1)求得f(x)的导数,由基本不等式可得斜率的最小值,及切点,运用点斜式方程可得切线的方程;(2)求出f(x)的导数,讨论判别式的符号,设出二次方程的两根,运用韦达定理和构造函数 ![]() ,x∈(0,1),求出导数,求得单调区间和极值、最值,即可得证.
,x∈(0,1),求出导数,求得单调区间和极值、最值,即可得证.
【考点精析】掌握函数的极值与导数是解答本题的根本,需要知道求函数![]() 的极值的方法是:(1)如果在
的极值的方法是:(1)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极大值(2)如果在
是极大值(2)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极小值.
是极小值.


 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案科目:高中数学 来源: 题型:
【题目】如图所示,正方形AA1D1D与矩形ABCD所在平面互相垂直,AB=2AD=2,点E为AB的中点. 
(1)求证:BD1∥平面A1DE;
(2)求直线A1E与平面AD1E所成角.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=lnax﹣ ![]() (a≠0).
(a≠0).
(1)求此函数的单调区间及最值;
(2)求证:对于任意正整数n,均有1+ ![]() +
+ ![]() …+
…+ ![]() ≥ln
≥ln ![]() (e为自然对数的底数).
(e为自然对数的底数).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设直线系M:xcosθ+ysinθ=1,对于下列四个命题:
①不在直线系M中的点都落在面积为π的区域内
②直线系M中所有直线为一组平行线
③直线系M中所有直线均经过一个定点
④对于任意整数n(n≥3),存在正n边形,其所有边均在直线系M中的直线上
其中真命题的代号是(写出所有真命题的代号).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分为16分)设A,B分别为椭圆![]()
![]() 的左、右顶点,椭圆的长轴长为
的左、右顶点,椭圆的长轴长为![]() ,且点
,且点![]() 在该椭圆上.
在该椭圆上.
(1)求椭圆的方程;
(2)设![]() 为直线
为直线![]() 上不同于点
上不同于点![]() 的任意一点,若直线
的任意一点,若直线![]() 与椭圆相交于异于
与椭圆相交于异于![]() 的点
的点![]() ,证明:△
,证明:△![]() 为钝角三角形.
为钝角三角形.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知F为抛物线y2=x的焦点,点A,B在该抛物线上且位于x轴的两侧, ![]() =2(其中O为坐标原点),则△ABO与△AFO面积之和的最小值是( )
=2(其中O为坐标原点),则△ABO与△AFO面积之和的最小值是( )
A.2
B.3
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在底面是正方形的四棱锥P﹣ABCD中,PA⊥面ABCD,BD交AC于点E,F是PC中点,G为AC上一点. 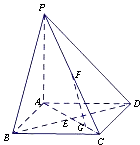
(1)求证:BD⊥FG;
(2)确定点G在线段AC上的位置,使FG∥平面PBD,并说明理由;
(3)当二面角B﹣PC﹣D的大小为 ![]() 时,求PC与底面ABCD所成角的正切值.
时,求PC与底面ABCD所成角的正切值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本题满分16分)数列![]() ,
, ![]() ,
, ![]() 满足:
满足: ![]() ,
, ![]() ,
, ![]() .
.
(1)若数列![]() 是等差数列,求证:数列
是等差数列,求证:数列![]() 是等差数列;
是等差数列;
(2)若数列![]() ,
, ![]() 都是等差数列,求证:数列
都是等差数列,求证:数列![]() 从第二项起为等差数列;
从第二项起为等差数列;
(3)若数列![]() 是等差数列,试判断当
是等差数列,试判断当![]() 时,数列
时,数列![]() 是否成等差数列?证明你的结论.
是否成等差数列?证明你的结论.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com