
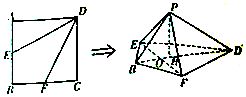
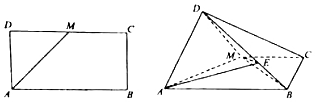
 如图,在正方形ABCD中,点E,F分别是AB,BC的中点,将△AED,△DCF分别沿DE,DF折起,使A,C两点重合于P.设EF与BD交于点O,过点P作PH⊥BD,垂足为H.
如图,在正方形ABCD中,点E,F分别是AB,BC的中点,将△AED,△DCF分别沿DE,DF折起,使A,C两点重合于P.设EF与BD交于点O,过点P作PH⊥BD,垂足为H.分析 (Ⅰ)推导出PD⊥PF,PD⊥PE,则PD⊥平面PEF,从而平面PBD⊥平面BFDE,由此能证明PH⊥底面BFDE.
(Ⅱ)设正方形ABCD的边长为x,推导出PO⊥PD,从而PH=$\frac{x}{3}$,由四棱锥P-BFDE的体积为12,求出正方形ABCD的边长为6.
解答 证明:(Ⅰ)由正方形ABCD知,∠DCF=∠DAE=90°,EF∥AC,BD⊥AC,EF⊥BD,
∵点E,F分别是AB,BC的中点.将△AED,△DCF分别沿DE,DF折起,使A,C两点重合于P.
∴PD⊥PF,PD⊥PE,
∵PE∩PF=P,PE、PF⊆平面PEF.
∴PD⊥平面PEF.
又∵EF?平面PEF,
∴PD⊥EF,又BD∩PD=D,
∴EF⊥平面PBD,
又EF?平面BFDE,∴平面PBD⊥平面BFDE.
∵平面PBD∩平面BFDE=BD,过点P作PH⊥BD,垂足为H,
∴PH⊥底面BFDE.
解:(Ⅱ)设正方形ABCD的边长为x,
则PD=x,PE=PF=$\frac{1}{2}x$,DB=$\sqrt{2}x$,DE=DF=$\frac{\sqrt{5}}{2}x$,EF=$\frac{\sqrt{2}}{2}x$,∠BPD=90°,
PO=$\sqrt{P{F}^{2}-O{F}^{2}}$=$\sqrt{\frac{1}{4}{x}^{2}-\frac{1}{8}{x}^{2}}$=$\frac{\sqrt{2}}{4}$x,OD=$\sqrt{\frac{5}{4}{x}^{2}-\frac{1}{8}{x}^{2}}$=$\frac{3\sqrt{2}}{4}$x,
∴PO2+PD2=OD2,∴PO⊥PD,
∴$\frac{1}{2}×OD×PH=\frac{1}{2}×OP×PD$,
∴PH=$\frac{OP×PD}{OD}$=$\frac{\frac{\sqrt{2}x}{4}×x}{\frac{3\sqrt{2}}{4}x}$=$\frac{x}{3}$,
∵四棱锥P-BFDE的体积为12,
∴VP-BFDE=$\frac{1}{3}×{S}_{四边形BFDE}×PH$=$\frac{1}{3}×\frac{1}{2}×BD×EF×PH$=$\frac{1}{6}×\sqrt{2}x×\frac{\sqrt{2}}{2}x×\frac{x}{3}$=12,
解得x=6.
∴正方形ABCD的边长为6.
点评 本题考查线面垂直的证明,考查正方形边长的求法,是基础题,解题时要认真审题,注意空间思维能力的培养.


科目:高中数学 来源: 题型:解答题
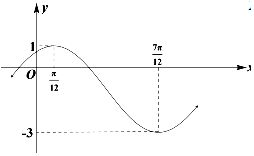 已知函数$f(x)=Asin(wx+φ)+B(A>0,w>0,|φ|<\frac{π}{2})$的 部分图象如图所示:
已知函数$f(x)=Asin(wx+φ)+B(A>0,w>0,|φ|<\frac{π}{2})$的 部分图象如图所示:查看答案和解析>>
科目:高中数学 来源: 题型:解答题
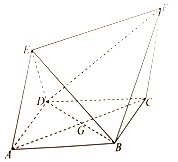 如图,四边形ABCD为菱形,四边形ACEF为平行四边形,设BD与AC相交于点G,AB=BD=2,AE=$\sqrt{3}$,∠EAD=∠EAB.
如图,四边形ABCD为菱形,四边形ACEF为平行四边形,设BD与AC相交于点G,AB=BD=2,AE=$\sqrt{3}$,∠EAD=∠EAB.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{500π}{81}$ | B. | 4π | C. | $\frac{25π}{9}$ | D. | $\frac{100π}{9}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
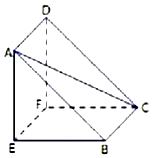 如图所示为一名曰“堑堵”的几何体,已知AE⊥底面BCFE,DF∥AE,DF=AE=1,CE=$\sqrt{7}$,四边形ABCD是正方形.
如图所示为一名曰“堑堵”的几何体,已知AE⊥底面BCFE,DF∥AE,DF=AE=1,CE=$\sqrt{7}$,四边形ABCD是正方形.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知椭圆$C:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的左、右顶点分别为A1,A2,左、右焦点分别为F1,F2,离心率为$\frac{1}{2}$,点B(4,0),F2为线段A1B的中点.
已知椭圆$C:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的左、右顶点分别为A1,A2,左、右焦点分别为F1,F2,离心率为$\frac{1}{2}$,点B(4,0),F2为线段A1B的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在四棱锥P-ABCD中,底面ABCD是长方形,侧棱PD⊥底面ABCD,且PD=AD=1,DC=2,过D作DF⊥PB于F,过F作FE⊥PB交PC于E.
如图,在四棱锥P-ABCD中,底面ABCD是长方形,侧棱PD⊥底面ABCD,且PD=AD=1,DC=2,过D作DF⊥PB于F,过F作FE⊥PB交PC于E.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com