
【题目】在平面直角坐标系![]() 中,点
中,点![]() ,直线
,直线![]() 与动直线
与动直线![]() 的交点为
的交点为![]() ,线段
,线段![]() 的中垂线与动直线
的中垂线与动直线![]() 的交点为
的交点为![]() .
.
(1)求动点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)过动点![]() 作曲线
作曲线![]() 的两条切线,切点分别为
的两条切线,切点分别为![]() ,
, ![]() ,求证:
,求证: ![]() 的大小为定值.
的大小为定值.

 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案科目:高中数学 来源: 题型:
【题目】已知等比数列{an}的前n项和Sn=2n+r.
(1)求实数r的值和{an}的通项公式;
(2)若数列{bn}满足b1=1,bn+1﹣bn=log2an+1 , 求bn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}的前n项和为Sn , 且a1=0,nan+1=Sn+n(n+1).
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)若数列{bn}满足an+log3n=log3bn , 求数列{bn}的前n项和Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某种产品的广告费支出x与销售额(单位:百万元)之间有如下对应数据:
如果y与x之间具有线性相关关系.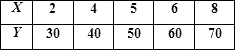
(1)作出这些数据的散点图;
(2)求这些数据的线性回归方程;
(3)预测当广告费支出为9百万元时的销售额.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
, ![]() .
.
(1)当![]() 时,求函数
时,求函数![]() 的单调增区间;
的单调增区间;
(2)设函数![]() ,
, ![]() .若函数
.若函数![]() 的最小值是
的最小值是![]() ,求
,求![]() 的值;
的值;
(3)若函数![]() ,
, ![]() 的定义域都是
的定义域都是![]() ,对于函数
,对于函数![]() 的图象上的任意一点
的图象上的任意一点![]() ,在函数
,在函数![]() 的图象上都存在一点
的图象上都存在一点![]() ,使得
,使得![]() ,其中
,其中![]() 是自然对数的底数,
是自然对数的底数, ![]() 为坐标原点.求
为坐标原点.求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在四棱锥P﹣ABCD中,PD⊥平面ABCD,底面是边长是1的正方形,侧棱PA与底面成45°的角,M,N,分别是AB,PC的中点; 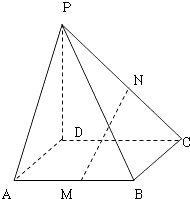
(1)求证:MN∥平面PAD;
(2)求四棱锥P﹣ABCD的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】把边长为2的正方形ABCD沿对角线BD折起并连接AC形成三棱锥C﹣ABD,其正视图、俯视图均为等腰直角三角形(如图所示),则三棱锥C﹣ABD的表面积为 . 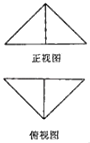
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com