练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】把边长为2的正方形ABCD沿对角线BD折起并连接AC形成三棱锥C﹣ABD，其正视图、俯视图均为等腰直角三角形（如图所示），则三棱锥C﹣ABD的表面积为 ．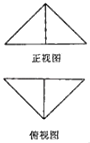

    【答案】4+2
    【解析】解：如图：∵正视图、俯视图均为全等的等腰直角三角形，
    ∴平面BCD⊥平面ABD，
    又O为BD的中点，∴CO⊥平面ABD，OA⊥平面BCD，
    三角形ACD与△ABC等式等边三角形，边长为2，所以面积相等为 ，
    又△ABD和△BCD面积和为正方形的面积4，
    ∴三棱锥C﹣ABD的表面积为2 +4；
    所以答案是：4+2 ．

    【考点精析】根据题目的已知条件，利用由三视图求面积、体积的相关知识可以得到问题的答案，需要掌握求体积的关键是求出底面积和高；求全面积的关键是求出各个侧面的面积．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】在平面直角坐标系中，点，直线与动直线的交点为，线段的中垂线与动直线的交点为．

    （1）求动点的轨迹的方程；

    （2）过动点作曲线的两条切线，切点分别为， ，求证： 的大小为定值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图给出的是计算 的值的一个程序框图，判断框内应填入的条件是（ ）

    A.i＜20
    B.i＞20
    C.i＜10
    D.i＞10

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】一个盒子装有六张卡片，上面分别写着如下六个函数： .

    （I）判断这个函数的奇偶性；

    （II）从中任意拿取两张卡片，若其中至少有一张卡片上写着的函数为奇函数.在此条件下，求两张卡片上写着的函数相加得到的新函数为奇函数的概率.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知抛物线的方程为： ，过点的一条直线与抛物线交于两点，若抛物线在两点的切线交于点.

    （1）求点的轨迹方程；

    （2）设直线的斜率存在，取为，取直线的斜率为，请验证是否为定值？若是，计算出该值；若不是，请说明理由.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在四棱锥P﹣ABCD中，已知PA⊥平面ABCD，AD∥BC，AD⊥AB，PA=AD=2BC=2AB=2．

    （1）求证：平面PAC⊥平面PCD；
    （2）若E是PD的中点，求平面BCE将四棱锥P﹣ABCD分成的上下两部分体积V1、V2之比．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知椭圆x2+4y2=4，直线l：y=x+m
    （1）若l与椭圆有一个公共点，求m的值；
    （2）若l与椭圆相交于P、Q两点，且|PQ|等于椭圆的短轴长，求m的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设△ABC的内角A、B、C所对边的长分别为a、b、c，则下列命题：
    ①若ab＞c2 ， 则C ；
    ②若a+b＞2c，则C ；
    ③若a3+b3=c3 ， 则C ；
    ④若（a+b）c＜2ab，则ab＞c2；
    ⑤若（a2+b2）c2＜2a2b2 ， 则C ．
    其中正确命题是（写出所有正确命题的序号）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图所示，已知长方体ABCD﹣A1B1C1D1中，AB=BC=2，AA1=4，E是棱CC1上的点，且BE⊥B1C．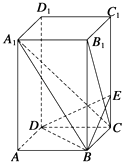

    （1）求CE的长；
    （2）求证：A1C⊥平面BED；
    （3）求A1B与平面BDE夹角的正弦值．

    查看答案和解析>>

    同步练习册答案