
【题目】如图所示,已知长方体ABCD﹣A1B1C1D1中,AB=BC=2,AA1=4,E是棱CC1上的点,且BE⊥B1C. 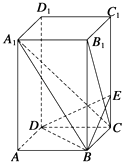
(1)求CE的长;
(2)求证:A1C⊥平面BED;
(3)求A1B与平面BDE夹角的正弦值.
【答案】
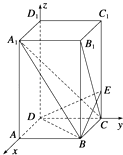
(1)解:如图所示,以D为原点,DA、DC、DD1所在直线分别为x、y、z轴建立空间直角坐标系D﹣xyz.
∴D(0,0,0),A(2,0,0),B(2,2,0),C(0,2,0),A1(2,0,4),
B1(2,2,4),C1(0,2,4),D1(0,0,4).
设E点坐标为(0,2,t),则 ![]() =(﹣2,0,t),
=(﹣2,0,t), ![]() =(﹣2,0,﹣4).
=(﹣2,0,﹣4).
∵BE⊥B1C,∴ ![]()
![]() =4+0﹣4t=0.
=4+0﹣4t=0.
∴t=1,故CE=1
(2)证明:由(1)得,E(0,2,1), ![]() =(﹣2,0,1),
=(﹣2,0,1),
又 ![]() =(﹣2,2,﹣4),
=(﹣2,2,﹣4), ![]() =(2,2,0)
=(2,2,0)
∴ ![]()
![]() =4+0﹣4=0,且
=4+0﹣4=0,且 ![]()
![]() =﹣4+4+0=0.
=﹣4+4+0=0.
∴ ![]() ⊥
⊥ ![]() 且
且 ![]() ⊥
⊥ ![]() ,即A1C⊥DB,A1C⊥BE,
,即A1C⊥DB,A1C⊥BE,
又∵DB∩BE=B,∴A1C⊥平面BDE,即A1C⊥平面BED
(3)解:由(2)知 ![]() =(﹣2,2,﹣4)是平面BDE的一个法向量.
=(﹣2,2,﹣4)是平面BDE的一个法向量.
又 ![]() =(0,2,﹣4),
=(0,2,﹣4),
∴cos< ![]() ,
, ![]() >=
>= 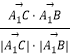 =
= ![]() .
.
∴A1B与平面BDE夹角的正弦值为 ![]() .
.
【解析】(1)建立空间直角坐标系,求出 ![]() 、
、 ![]() ,利用
,利用 ![]()
![]() =0,即可求得结论;(2)证明
=0,即可求得结论;(2)证明 ![]() ⊥
⊥ ![]() 且
且 ![]() ⊥
⊥ ![]() ,可得A1C⊥DB,A1C⊥BE,从而可得A1C⊥平面BED;(3)由(2)知
,可得A1C⊥DB,A1C⊥BE,从而可得A1C⊥平面BED;(3)由(2)知 ![]() =(﹣2,2,﹣4)是平面BDE的一个法向量,利用向量的夹角公式,即可求A1B与平面BDE夹角的正弦值.
=(﹣2,2,﹣4)是平面BDE的一个法向量,利用向量的夹角公式,即可求A1B与平面BDE夹角的正弦值.
【考点精析】利用直线与平面垂直的判定和空间角的异面直线所成的角对题目进行判断即可得到答案,需要熟知一条直线与一个平面内的两条相交直线都垂直,则该直线与此平面垂直;注意点:a)定理中的“两条相交直线”这一条件不可忽视;b)定理体现了“直线与平面垂直”与“直线与直线垂直”互相转化的数学思想;已知![]() 为两异面直线,A,C与B,D分别是
为两异面直线,A,C与B,D分别是![]() 上的任意两点,
上的任意两点,![]() 所成的角为
所成的角为![]() ,则
,则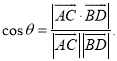 .
.


科目:高中数学 来源: 题型:
【题目】把边长为2的正方形ABCD沿对角线BD折起并连接AC形成三棱锥C﹣ABD,其正视图、俯视图均为等腰直角三角形(如图所示),则三棱锥C﹣ABD的表面积为 . 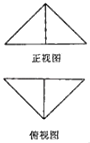
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(理)如图,在四棱锥S﹣ABCD中,底面ABCD是边长为1的正方形,S到A、B、C、D的距离都等于2.给出以下结论:
① ![]() +
+ ![]() +
+ ![]() +
+ ![]() =
= ![]() ;
;
② ![]() +
+ ![]() ﹣
﹣ ![]() ﹣
﹣ ![]() =
= ![]() ;
;
③ ![]() ﹣
﹣ ![]() +
+ ![]() ﹣
﹣ ![]() =
= ![]() ;
;
④ ![]()
![]() =
= ![]()
![]() ;
;
⑤ ![]()
![]() =0,
=0,
其中正确结论是( )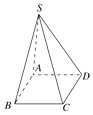
A.①②③
B.④⑤
C.②④
D.③④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥![]() 中,底面
中,底面![]() 是矩形,平面
是矩形,平面![]() 平面
平面![]() ,且
,且![]() 是边长为
是边长为![]() 的等边三角形,
的等边三角形, ![]() ,点
,点![]() 是
是![]() 的中点.
的中点.
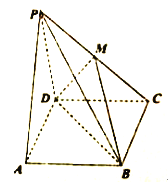
(1)求证: ![]() 平面
平面![]() ;
;
(2)点![]() 在
在![]() 上,且满足
上,且满足![]() ,求直线
,求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,过椭圆
中,过椭圆![]() 右焦点
右焦点![]() 的直线
的直线![]() 交椭圆
交椭圆![]() 于
于![]() 两点 ,
两点 , ![]() 为
为![]() 的中点,且
的中点,且![]() 的斜率为
的斜率为![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)设过点![]() 的直线
的直线![]() (不与坐标轴垂直)与椭圆
(不与坐标轴垂直)与椭圆![]() 交于
交于![]() 两点,问:在
两点,问:在![]() 轴上是否存在定点
轴上是否存在定点![]() ,使得
,使得![]() 为定值?若存在,求出点
为定值?若存在,求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某小学对五年级的学生进行体质测试,已知五年一班共有学生30人,测试立定跳远的成绩用茎叶图表示如图(单位:cm): 男生成绩在175cm以上(包括175cm)定义为“合格”,成绩在175cm以下(不包括175cm)定义为“不合格”.
女生成绩在165cm以上(包括165cm)定义为“合格”,成绩在165cm以下(不包括165cm)定义为“不合格”.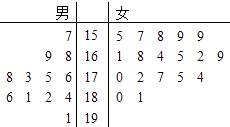
(1)求五年一班的女生立定跳远成绩的中位数;
(2)在五年一班的男生中任意选取3人,求至少有2人的成绩是合格的概率;
(3)若从五年一班成绩“合格”的学生中选取2人参加复试,用X表示其中男生的人数,写出X的分布列,并求X的数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
: ![]() 的短轴长为
的短轴长为![]() ,右焦点为
,右焦点为![]() ,点
,点![]() 是椭圆
是椭圆![]() 上异于左、右顶点
上异于左、右顶点![]() 的一点.
的一点.
(1)求椭圆![]() 的方程;
的方程;
(2)若直线![]() 与直线
与直线![]() 交于点
交于点![]() ,线段
,线段![]() 的中点为
的中点为![]() ,证明:点
,证明:点![]() 关于直线
关于直线![]() 的对称点在直线
的对称点在直线![]() 上.
上.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com