练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知函数 .

    （1）若 ，求曲线 在点 处的切线方程；

    （2）若对任意 在恒成立，求实数的取值范围.

    【答案】（1）（2）

    【解析】试题分析：

    (1)利用题意可得切线斜率 ，切点为 ，所以曲线 在点处的切线方程为 .

    (2)将问题转化为不等式恒成立，分类讨论可得实数 的取值范围为 .

    试题解析：

    解：(1)当 时， ，则 ，故切线斜率 ，又因为切点为 ，所以曲线 在点处的切线方程为，即 .

    (2)不等式等价于不等式，记，则 ，令 ，得 或 .

    ①当，即时 ， ，所以在单调递增，所以，解得，此时.

    ②当时，即 ， 时， ， 时， ，所以

    函数在上单调递减，在上单调递增，于是 ，不合题意，舍去.

    综上所述，实数 的取值范围为 .

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】如图，在四棱锥P﹣ABCD中，已知PA⊥平面ABCD，AD∥BC，AD⊥AB，PA=AD=2BC=2AB=2．

    （1）求证：平面PAC⊥平面PCD；
    （2）若E是PD的中点，求平面BCE将四棱锥P﹣ABCD分成的上下两部分体积V1、V2之比．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图是一块地皮，其中， 是直线段，曲线段是抛物线的一部分，且点是该抛物线的顶点， 所在的直线是该抛物线的对称轴．经测量， km， km， ．现要从这块地皮中划一个矩形来建造草坪，其中点在曲线段上，点， 在直线段上，点在直线段上，设km，矩形草坪的面积为km2．

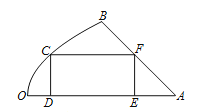
    （1）求，并写出定义域；

    （2）当为多少时，矩形草坪的面积最大？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，边长为2的正方形ABCD中，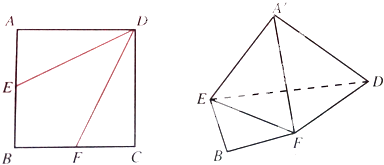

    （1）点E是AB的中点，点F是BC的中点，将△AED，△DCF分别沿DE，DF折起，使A，C两点重合于点A′．求证：A′D⊥EF
    （2）当BE=BF= BC时，求三棱锥A′﹣EFD的体积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图所示，已知长方体ABCD﹣A1B1C1D1中，AB=BC=2，AA1=4，E是棱CC1上的点，且BE⊥B1C．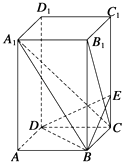

    （1）求CE的长；
    （2）求证：A1C⊥平面BED；
    （3）求A1B与平面BDE夹角的正弦值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】一扇形的周长为20cm，当扇形的圆心角α等于多少时，这个扇形的面积最大？最大面积是多少？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设函数F（x）= ，其中f（x）=log2（x2+1），g（x）=log2（|x|+7）．
    （1）在实数集R上用分段函数形式写出函数F（x）的解析式；
    （2）求函数F（x）的最小值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知椭圆C： =1（a＞b＞0）的离心率为 ，以原点为圆心，椭圆的短半轴为半径的圆与直线x﹣y+ =0相切，过点P（4，0）且不垂直于x轴直线l与椭圆C相交于A、B两点．
    （1）求椭圆C的方程；
    （2）求 的取值范围；
    （3）若B点关于x轴的对称点是E，证明：直线AE与x轴相交于定点．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知a为正的常数，函数f（x）=|ax﹣x2|+lnx．
    （1）若a=2，求函数f（x）的单调递增区间；
    （2）设g（x）= ，求g（x）在区间[1，e]上的最小值．（e≈2.71828为自然对数的底数）

    查看答案和解析>>

    同步练习册答案