
【题目】设函数F(x)= ![]() ,其中f(x)=log2(x2+1),g(x)=log2(|x|+7).
,其中f(x)=log2(x2+1),g(x)=log2(|x|+7).
(1)在实数集R上用分段函数形式写出函数F(x)的解析式;
(2)求函数F(x)的最小值.
【答案】
(1)
解:F(x)= 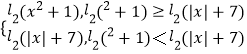 ,
,
令log2(x2+1)≥log2(|x|+7),得x2﹣|x|﹣6≥0,
解得:x≤﹣3或x≥3,(5分)∴F(x)= 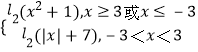
(2)
解:当x≥3或x≤﹣3时,F(x)=log2(x2+1),设u=x2+1≥10,y=log2u在[10,+∞)上递增,所以F(x)min=log210;(说明:设元及单调性省略不扣分)
同理,当﹣3<x<3,F(x)min=log27;
又log27<log210∴x∈R时,F(x)min=log27.
或解:因为F(x)是偶函数,所以只需要考虑x≥0的情形,
当0≤x<3,F(x)=log2(x2+7),当x=0时,F(x)min=log27;
当x≥3时,F(x)=log2(x2+1),当x=3时,F(x)min=log210;
∴x∈R时,F(x)min=log27
【解析】(1)令log2(x2+1)≥log2(|x|+7),解得:x的取值范围,再结合F(x)的意义用分段函数形式写出函数F(x)的解析式即可;(2)先分情况讨论函数的单调性:当x≥3或x≤﹣3时;当﹣3<x<3,分别求出F(x)的最小值,最后综合得出x∈R时,F(x)min=log27.或利用F(x)的奇偶性,只需要考虑x≥0的情形,只须分两种情形讨论:当0≤x<3,当x≥3时,分别求得F(x)的最小值即得.
【考点精析】关于本题考查的函数的值域,需要了解求函数值域的方法和求函数最值的常用方法基本上是相同的.事实上,如果在函数的值域中存在一个最小(大)数,这个数就是函数的最小(大)值.因此求函数的最值与值域,其实质是相同的才能得出正确答案.


科目:高中数学 来源: 题型:
【题目】如图,四棱锥![]() 中,底面
中,底面![]() 是矩形,平面
是矩形,平面![]() 平面
平面![]() ,且
,且![]() 是边长为
是边长为![]() 的等边三角形,
的等边三角形, ![]() ,点
,点![]() 是
是![]() 的中点.
的中点.
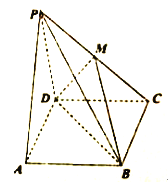
(1)求证: ![]() 平面
平面![]() ;
;
(2)点![]() 在
在![]() 上,且满足
上,且满足![]() ,求直线
,求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】关于平面向量,有下列四个命题:
①若 ![]() .
.
② ![]() =(1,1),
=(1,1), ![]() =(2,x),若
=(2,x),若 ![]() 与
与 ![]() 平行,则x=2.
平行,则x=2.
③非零向量 ![]() 和
和 ![]() 满足|
满足| ![]() |=|
|=| ![]() |=|
|=| ![]() |,则
|,则 ![]() 与
与 ![]() 的夹角为60°.
的夹角为60°.
④点A(1,3),B(4,﹣1),与向量 ![]() 同方向的单位向量为(
同方向的单位向量为( ![]() ).
).
其中真命题的序号为 . (写出所有真命题的序号)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某小学对五年级的学生进行体质测试,已知五年一班共有学生30人,测试立定跳远的成绩用茎叶图表示如图(单位:cm): 男生成绩在175cm以上(包括175cm)定义为“合格”,成绩在175cm以下(不包括175cm)定义为“不合格”.
女生成绩在165cm以上(包括165cm)定义为“合格”,成绩在165cm以下(不包括165cm)定义为“不合格”.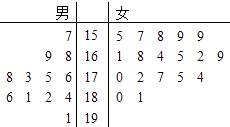
(1)求五年一班的女生立定跳远成绩的中位数;
(2)在五年一班的男生中任意选取3人,求至少有2人的成绩是合格的概率;
(3)若从五年一班成绩“合格”的学生中选取2人参加复试,用X表示其中男生的人数,写出X的分布列,并求X的数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com