
【题目】设△ABC的内角A、B、C所对边的长分别为a、b、c,则下列命题:
①若ab>c2 , 则C ![]() ;
;
②若a+b>2c,则C ![]() ;
;
③若a3+b3=c3 , 则C ![]() ;
;
④若(a+b)c<2ab,则ab>c2;
⑤若(a2+b2)c2<2a2b2 , 则C ![]() .
.
其中正确命题是(写出所有正确命题的序号).
【答案】①②③
【解析】解:①ab>c2cosC= ![]() >
> ![]() =
= ![]() C<
C< ![]() ,故①正确;②a+b>2ccosC=
,故①正确;②a+b>2ccosC= ![]() >
> ![]() ≥
≥ ![]() ×
× ![]() ﹣
﹣ ![]() ≥
≥ ![]() =
= ![]() C<
C< ![]() ,故②正确;③∵a3+b3=c3 , ∴(
,故②正确;③∵a3+b3=c3 , ∴( ![]() )3+(
)3+( ![]() )3=1,即0<
)3=1,即0< ![]() <1,0<
<1,0< ![]() <1,
<1,
则1=( ![]() )3+(
)3+( ![]() )3<(
)3<( ![]() )2+(
)2+( ![]() )2 , 即c2<a2+b2 , 故C
)2 , 即c2<a2+b2 , 故C ![]() ;故③正确;④⑤取a=b=2,c=1,满足(a+b)c<2ab,(a2+b2)c2<2a2b2成立得:C<
;故③正确;④⑤取a=b=2,c=1,满足(a+b)c<2ab,(a2+b2)c2<2a2b2成立得:C< ![]() <
< ![]() ,故④⑤错误;
,故④⑤错误;
所以答案是:①②③.
【考点精析】本题主要考查了命题的真假判断与应用的相关知识点,需要掌握两个命题互为逆否命题,它们有相同的真假性;两个命题为互逆命题或互否命题,它们的真假性没有关系才能正确解答此题.


科目:高中数学 来源: 题型:
【题目】把边长为2的正方形ABCD沿对角线BD折起并连接AC形成三棱锥C﹣ABD,其正视图、俯视图均为等腰直角三角形(如图所示),则三棱锥C﹣ABD的表面积为 . 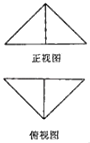
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(理)如图,在四棱锥S﹣ABCD中,底面ABCD是边长为1的正方形,S到A、B、C、D的距离都等于2.给出以下结论:
① ![]() +
+ ![]() +
+ ![]() +
+ ![]() =
= ![]() ;
;
② ![]() +
+ ![]() ﹣
﹣ ![]() ﹣
﹣ ![]() =
= ![]() ;
;
③ ![]() ﹣
﹣ ![]() +
+ ![]() ﹣
﹣ ![]() =
= ![]() ;
;
④ ![]()
![]() =
= ![]()
![]() ;
;
⑤ ![]()
![]() =0,
=0,
其中正确结论是( )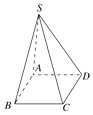
A.①②③
B.④⑤
C.②④
D.③④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥![]() 中,底面
中,底面![]() 是矩形,平面
是矩形,平面![]() 平面
平面![]() ,且
,且![]() 是边长为
是边长为![]() 的等边三角形,
的等边三角形, ![]() ,点
,点![]() 是
是![]() 的中点.
的中点.
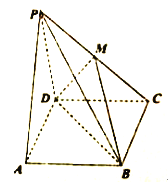
(1)求证: ![]() 平面
平面![]() ;
;
(2)点![]() 在
在![]() 上,且满足
上,且满足![]() ,求直线
,求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某小学对五年级的学生进行体质测试,已知五年一班共有学生30人,测试立定跳远的成绩用茎叶图表示如图(单位:cm): 男生成绩在175cm以上(包括175cm)定义为“合格”,成绩在175cm以下(不包括175cm)定义为“不合格”.
女生成绩在165cm以上(包括165cm)定义为“合格”,成绩在165cm以下(不包括165cm)定义为“不合格”.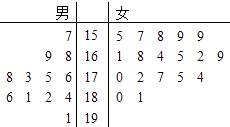
(1)求五年一班的女生立定跳远成绩的中位数;
(2)在五年一班的男生中任意选取3人,求至少有2人的成绩是合格的概率;
(3)若从五年一班成绩“合格”的学生中选取2人参加复试,用X表示其中男生的人数,写出X的分布列,并求X的数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com