
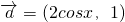 、
、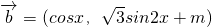 ,
, .
.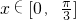 时,f(x)的最大值为6,求实数m的值.
时,f(x)的最大值为6,求实数m的值. =
= =2
=2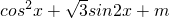
 sin2x+m+1=2sin(2x+
sin2x+m+1=2sin(2x+ )+m+1.
)+m+1. ≤2x+
≤2x+ ≤2kπ+
≤2kπ+ ,k∈z,可得 kπ-
,k∈z,可得 kπ- ≤x≤kπ+
≤x≤kπ+ ,故函数在[0,π]上的增区间为
,故函数在[0,π]上的增区间为  ],[
],[ ,π].
,π].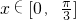 时,2x+
时,2x+ ∈[
∈[ ,
, ],故当2x+
],故当2x+ =
= ,即 x=
,即 x= 时,
时, )+m+1,由
)+m+1,由 ≤2x+
≤2x+ ≤2kπ+
≤2kπ+ ,k∈z,求出函数在[0,π]上的增区间.
,k∈z,求出函数在[0,π]上的增区间.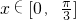 时,2x+
时,2x+ ∈[
∈[ ,
, ],故当2x+
],故当2x+ =
= ,f(x)=2+m+1 的值为6,由此求得m 值
,f(x)=2+m+1 的值为6,由此求得m 值

科目:高中数学 来源: 题型:
| 2m-1-mx | x+1 |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 | |2x-b| |
查看答案和解析>>
科目:高中数学 来源: 题型:
(1)求图象的开口方向、对称轴、顶点坐标、与x轴的交点坐标;
(2)求函数的单调区间、最值和零点;
(3)设图象与x轴相交于(x1,0)、(x2,0),不求出根,求|x1-x2|;
(4)已知f(-![]() )=
)=![]() ,不计算函数值,求f(-
,不计算函数值,求f(-![]() );
);
(5)不计算函数值,试比较f(-![]() )与f(-
)与f(-![]() )的大小;
)的大小;
(6)写出使函数值为负数的自变量x的集合.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com