
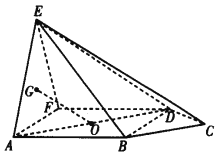
【题目】如图所示,在五棱锥![]() 中,侧面
中,侧面![]() 底面
底面![]() ,
,![]() 是边长为2的正三角形,四边形
是边长为2的正三角形,四边形![]() 为正方形,
为正方形,![]() ,且
,且![]() ,
,![]() 是
是![]() 的重心,
的重心,![]() 是正方形
是正方形![]() 的中心.
的中心.
(Ⅰ)求证:![]() 平面
平面![]() ;
;
(Ⅱ)求二面角![]() 的余弦值.
的余弦值.
【答案】(Ⅰ)见解析;(Ⅱ)![]()
【解析】
(1)证明线面平行,转化为线线平行.取![]() 中点
中点![]() ,
,![]() 中点
中点![]() ,连接
,连接![]() ,
,![]() 即可.(2)求二面角
即可.(2)求二面角![]() 的余弦值,以
的余弦值,以![]() 为原点,以
为原点,以![]() 方向为
方向为![]() 轴正方向,以
轴正方向,以![]() 方向为
方向为![]() 轴正方向,以
轴正方向,以![]() 方向为
方向为![]() 轴正方向,建立空间直角坐标系即可.
轴正方向,建立空间直角坐标系即可.
(Ⅰ)取![]() 中点
中点![]() ,
,![]() 中点
中点![]() ,连接
,连接![]() ,
,![]() ,易知
,易知![]() ,
,![]() ,
,![]() ,
,![]() 四点共线.
四点共线.
由![]() ,且
,且![]() ,可知
,可知![]() 为等腰直角三角形,所以
为等腰直角三角形,所以![]() .
.
因为![]() 是正方形
是正方形![]() 的中心,所以
的中心,所以![]() .
.
所以![]() ,所以
,所以![]() .又
.又![]() 是
是![]() 的重心,所以
的重心,所以![]() .
.
所以![]() ,故
,故![]() .又因为
.又因为![]() 平面
平面![]() ,
,![]() 平面
平面![]() .
.
所以![]() 平面
平面![]() .
.
(Ⅱ)解法一:因为![]() 为中点,
为中点,![]() 是正三角形,所以
是正三角形,所以![]() .
.
因为侧面![]() 底面
底面![]() ,且交线为
,且交线为![]() ,所以
,所以![]() 底面
底面![]() .所以直线
.所以直线![]() ,
,![]() ,
,![]() 两两垂直.
两两垂直.
如图,以![]() 为原点,以
为原点,以![]() 方向为
方向为![]() 轴正方向,以
轴正方向,以![]() 方向为
方向为![]() 轴正方向,以
轴正方向,以![]() 方向为
方向为![]() 轴正方向,建立空间直角坐标系.
轴正方向,建立空间直角坐标系.

则![]() ,
,![]() ,
,![]() ,
,![]() .所以
.所以![]() ,
,![]() ,
,![]() .
.
设平面![]() 的法向量为
的法向量为![]() ,
,
则 令
令![]() ,则
,则![]() .
.
设平面![]() 的法向量为
的法向量为![]() ,
,
则 ,令
,令![]() ,则
,则![]() .
.
所以 .
.
结合图可知,二面角![]() 的余弦值为
的余弦值为![]() .
.
解法二:取![]() ,
,![]() 中点分别为
中点分别为![]() ,
,![]() ,连接
,连接![]() ,
,![]() ,则
,则![]() .
.
又侧面![]() 底面
底面![]() ,
,![]() ,侧面
,侧面![]() 底面
底面![]() ,所以
,所以![]() 平面
平面![]() .
.
又![]() 平面
平面![]() ,所以
,所以![]() ,所以
,所以![]() .
.
又![]() ,
,![]() ,所以
,所以![]() ,所以
,所以![]() .
.
所以![]() 为二面角
为二面角![]() 的平面角.
的平面角.
易知![]() ,所以
,所以![]() .因为
.因为![]() ,
,![]() ,
,
所以![]() ,所以
,所以![]() .
.
即二面角![]() 的余弦值为
的余弦值为![]() .
.



科目:高中数学 来源: 题型:
【题目】如图,三棱柱![]() 的侧面
的侧面![]() 是平行四边形,
是平行四边形,![]() ,平面
,平面![]() 平面
平面![]() ,且
,且![]() 分别是
分别是![]() 的中点.
的中点.

(Ⅰ)求证:![]() ;
;
(Ⅱ)求证:![]() 平面
平面![]() ;
;
(Ⅲ)在线段![]() 上是否存在点
上是否存在点![]() ,使得
,使得![]() 平面
平面![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“科技引领,布局未来”科技研发是企业发展的驱动力量.2007年至2018年,某企业连续12年累计研发投入达4100亿元,我们将研发投入与经营收入的比值记为研发投入占营收比.这12年间的研发投入(单位:十亿元)用图中的条形图表示,研发投入占营收比用图中的折线图表示.

根据折线图和条形图,下列结论错误的是( )
A. 2012﹣2013 年研发投入占营收比增量相比 2017﹣2018 年增量大
B. 该企业连续 12 年研发投入逐年增加
C. 2015﹣2016 年研发投入增值最大
D. 该企业连续 12 年研发投入占营收比逐年增加
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,等腰梯形ABCD中,AB∥CD,AD=AB=BC=1,CD=2,E为CD中点,AE与BD交于点O,将△ADE沿AE折起,使点D到达点P的位置(P平面ABCE).
(Ⅰ)证明:平面POB⊥平面ABCE;
(Ⅱ)若直线PB与平面ABCE所成的角为![]() ,求二面角A-PE-C的余弦值.
,求二面角A-PE-C的余弦值.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2013年华人数学家张益唐证明了孪生素数猜想的一个弱化形式。孪生素数猜想是希尔伯特在1900年提出的23个问题之一,可以这样描述:存在无穷多个素数p,使得p+2是素数,素数对(p,p+2)称为孪生素数.在不超过30的素数中,随机选取两个不同的数,其中能够组成孪生素数的概率是
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知圆锥的顶点为S,底面圆O的两条直径分别为AB和CD,且AB⊥CD,若平面![]() 平面
平面![]() .现有以下四个结论:
.现有以下四个结论:

①AD∥平面SBC;
②![]() ;
;
③若E是底面圆周上的动点,则△SAE的最大面积等于△SAB的面积;
④![]() 与平面SCD所成的角为45°.
与平面SCD所成的角为45°.
其中正确结论的序号是__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示的几何体,是将高为2、底面半径为1的圆柱沿过旋转轴的平面切开后,将其中一半沿切面向右水平平移后形成的封闭体.![]() 分别为
分别为![]() 的中点,
的中点,![]() 为弧
为弧![]() 的中点,
的中点,![]() 为弧
为弧![]() 的中点.
的中点.
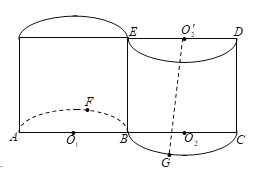
(1)求直线![]() 与底面
与底面![]() 所成的角的大小;
所成的角的大小;
(2)求异面直线![]() 与
与![]() 所成的角的大小(结果用反三角函数值表示).
所成的角的大小(结果用反三角函数值表示).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com