
【题目】为对考生的月考成绩进行分析,某地区随机抽查了 ![]() 名考生的成绩,根据所得数据画了如下的样本频率分布直方图.
名考生的成绩,根据所得数据画了如下的样本频率分布直方图.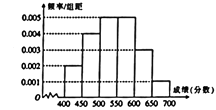
(1)求成绩在 ![]() 的频率;
的频率;
(2)根据频率分布直方图算出样本数据的中位数;
(3)为了分析成绩与班级、学校等方面的关系,必须按成绩再从这 ![]() 人中用分层抽样方法抽取出
人中用分层抽样方法抽取出 ![]() 人作出进一步分析,则成绩在
人作出进一步分析,则成绩在 ![]() 的这段应抽多少人?
的这段应抽多少人?
【答案】
(1)解:根据频率分布直方图,得:成绩在[600,650)的频率为
0.003×(650﹣600)=0.15。
(2)解: f 1 = 0.002 × 50 = 0.1 … f 2 = 0.004 × 50 = 0.2 … f 3 = 0.005 × 50 = 0.25 ,
f 4 = 0.005 × 50 = 0.25 … f 5 = 0.003 × 50 = 0.15 … f 6 = 0.001 × 50 = 0.05,
0.1 × 425 + 0.2 × 475 + 0.25 × 525 + 0.25 × 575 + 0.15 × 625 + 0.05 × 675 = 540。
(3)解:成绩在[550,600)的频率为:0.005×(600﹣550)=0.25,
所以10000名考生中成绩在[550,600)的人数为:0.25×10000=2500(人),
再从10000人用分层抽样方法抽出20人,
则成绩在[550,600)的这段应抽取20× ![]() =5人。
=5人。
【解析】(1)考查对频率分布直方图的理解能力。
(2)主要考查中位数的相关性质,即将统计总数当中的各个变量值按大小顺序排列起来,形成一个数列,处于变量数列中间位置的变量值称为中位数。其中,当变量值的项数为奇数时,处于中间位置的变量值即为中位数;当变量值的项数为偶数时,中位数则为处于中间位置的2个变量值的平均数。
(3)主要考查分层抽样的相关性质,分层抽样要求将总体的单位按某种特征分为若干次级层,然后再从每一层内进行随机抽样。


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】在扶贫活动中,为了尽快脱贫(无债务)致富,企业甲将经营状况良好的某种消费品专卖店以5.8万元的优惠价格转让给了尚有5万元无息贷款没有偿还的小型企业乙,并约定从该店经营的利润中,首先保证企业乙的全体职工每月最低生活费的开支3 600元后,逐步偿还转让费(不计息).在甲提供的资料中:①这种消费品的进价为每件14元;②该店月销量Q(百件)与销售价格P(元)的关系如图所示;③每月需各种开支2 000元.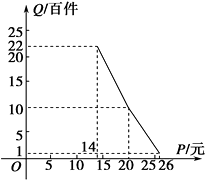
(1)当商品的价格为每件多少元时,月利润扣除职工最低生活费的余额最大?并求最大余额;
(2)企业乙只依靠该店,最早可望在几年后脱贫?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)= ![]() ,若方程f(f(x))=a(a>0)恰有两个不相等的实根x1 , x2 , 则e
,若方程f(f(x))=a(a>0)恰有两个不相等的实根x1 , x2 , 则e ![]() e
e ![]() 的最大值为( )
的最大值为( )
A.![]()
B.2(ln2﹣1)
C.![]()
D.ln2﹣1
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若函数 ![]() ,
, ![]() ,对于给定的非零实数
,对于给定的非零实数 ![]() ,总存在非零常数
,总存在非零常数 ![]() ,使得定义域
,使得定义域 ![]() 内的任意实数
内的任意实数 ![]() ,都有
,都有 ![]() 恒成立,此时
恒成立,此时 ![]() 为
为 ![]() 的类周期,函数
的类周期,函数 ![]() 是
是 ![]() 上的
上的 ![]() 级类周期函数.若函数
级类周期函数.若函数 ![]() 是定义在区间
是定义在区间 ![]() 内的2级类周期函数,且
内的2级类周期函数,且 ![]() ,当
,当 ![]() 时,
时, 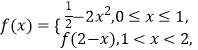 函数
函数 ![]() .若
.若 ![]() ,
, ![]() ,使
,使 ![]() 成立,则实数
成立,则实数 ![]() 的取值范围是( )
的取值范围是( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国古代数学名著《算法统宗》中有如下问题:“远望巍巍塔七层,红光点点倍加增,共灯三百八十一,请问尖头几盏灯?”意思是:一座7层塔共挂了381盏灯,且相邻两层中的下一层灯数是上一层灯数的2倍,则塔的顶层共有灯( )
A.1盏
B.3盏
C.5盏
D.9盏
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥 ![]() 中,底面梯形
中,底面梯形 ![]() ,
, ![]() ,平面
,平面 ![]() 平面
平面 ![]() ,
, ![]() 是等边三角形,已知
是等边三角形,已知 ![]() ,
, ![]() ,
, ![]() 是
是 ![]() 上任意一点,
上任意一点, ![]() ,且
,且 ![]() .
.
(1)求证:平面 ![]() 平面
平面 ![]() ;
;
(2)试确定 ![]() 的值,使三棱锥
的值,使三棱锥 ![]() 体积为三棱锥
体积为三棱锥 ![]() 体积的3倍.
体积的3倍.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数 ![]() (其中
(其中 ![]() ,
, ![]() 为常数,
为常数, ![]() 为自然对数的底数).
为自然对数的底数).
(1)讨论函数 ![]() 的单调性;
的单调性;
(2)设曲线 ![]() 在
在 ![]() 处的切线为
处的切线为 ![]() ,当
,当 ![]() 时,求直线
时,求直线 ![]() 在
在 ![]() 轴上截距的取值范围.
轴上截距的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com