练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
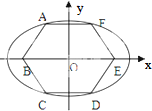
    如图正六边形ABCDEF中，B、E为椭圆的焦点，A、C、D、F在椭圆上，则椭圆的离心率为（　　）
    A、
    		3
    -1
    B、
    		3
    -1
    2
    C、
    		3
    2
    -1
    D、
    1
    2
    考点：椭圆的简单性质
    专题：计算题,圆锥曲线的定义、性质与方程
    分析：连接BF，则BF⊥FE．设|BE|=2c，则可求得FE和BF，进而由椭圆的定义知2a=|BF|+|FE|=
    		3
    c+c，最后根据离心率公式求得答案．
    解答： 解：连接BF，则BF⊥FE．设|BE|=2c，则|FE|=c，|BF|=
    		3
    c．
    椭圆定义，得2a=|BF|+|FE|=
    		3
    c+c，
    所以e=
    c
    a
    =
    2
    		3
    +1
    =
    		3
    -1，
    故选：A．
    点评：本题主要考查了椭圆的简单性质．特别是椭圆定义的应用．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    如图所示，平行六面体ABCD-A1B1C1D1中，以顶点A为端点的三条棱长都为1，且两两夹角为60°，则AC1的长为（　　）
    A、1
    B、
    		3
    C、2
    		2
    D、
    		6

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    PM2.5是指大气中直径小于或等于2.5微米的颗粒物，也称为可A肺颗粒物，般情况下PM2.5浓度越大，大气环境质量越差，茎叶图表示的是成都市区甲、乙两个监测站某10日内每天的PM2.5浓度读数（单位：μg/m3）则下列说法正确的是（　　）
    A、这l0日内甲、乙监测站读数的极差相等
    B、这10日内甲、乙监测站读数的中位数中，乙的较大
    C、这10日内乙监测站读数的众数与中位数相等
    D、这10日内甲、乙监测站读数的平均数相等

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知点A（0，1）是椭圆x2+4y2=4上的一点，P点是椭圆上的动点，则弦AP长度的最大值为（　　）
    A、
    2
    		3
    3
    B、2
    C、
    4
    		3
    3
    D、4

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知命题p：?x∈R，x2-2x+1＞0；命题q：?x∈R，sinx=1，则下列判断正确的是（　　）
    A、p是真命题
    B、￢q是假命题
    C、￢p是假命题
    D、q是假命题

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知双曲线C：
    x2
    a2
    -
    y2
    b2
    =1（a＞0，b＞0）的焦距为6，两顶点之间的距离为2，则C的方程为（　　）
    A、
     x2
    8
    -
    y2
    9
    =1
    B、
    x2
    8
    -y2=1
    C、x2-
    y2
    8
    =1
    D、
    x2
    9
    -
    y2
    8
    =1

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知f（n）=1+
    1
    2
    +
    1
    3
    +…+
    1
    n
    （n∈N*），计算得f（2）=
    3
    2
    ，f（4）＞2，f（8）＞
    5
    2
    ，f（16）＞3，f（32）＞
    7
    2
    ，由此推算：当n≥2时，有（　　）
    A、f（2n）＞
    2n+1
    2
    （n∈N*）
    B、f（2n）＞
    2(n+1)-1
    2
    （n∈N*）
    C、f（2n）＞
    2n+1
    2
    （n∈N*）
    D、f（2n）＞
    n+2
    2
    （n∈N*）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    执行如图所示的程序框图，若输出k=2，则输入x的取值范围是（　　）
    A、（28，57]
    B、[28，57）
    C、（28，57）
    D、[28，57]

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    如图，△ABC的AB边长为2，P，Q分别是AC，BC中点，记
    AB
    •
    AP
    +
    BA
    •
    BQ
    =m，
    AB
    •
    AQ
    +
    BA
    •
    BP
    =n，则（　　）
    A、m=2，n=4
    B、m=3，n=1
    C、m=2，n=6
    D、m=3n，但m，n的值不确定

    查看答案和解析>>

    同步练习册答案