Question

18．在平行六面体ABCD-A₁B₁C₁D₁中，若AA₁=AB=AD=1，∠A₁AD=∠A₁AB=∠BAD=60°，则直线AC₁与平面ABCD所成的角的余弦值为（　　）

• A． $\frac{{\sqrt{2}}}{3}$
• B． $\frac{{2\sqrt{2}}}{3}$
• C． $\frac{{\sqrt{3}}}{3}$
• D． $\frac{{\sqrt{6}}}{3}$

Answer 1

分析 由已知条件A₁在底面ABCD上的射影在AC上，设为E，C₁在底面ABCD上的射影在AC延长线上，设为F，并过E作EG⊥AB，连接A₁G，便有A₁G⊥AB，从而根据已知的边角值，分别在直角三角形中即可求出AE，A₁E，连接BD与AC交于O，从而有BD⊥AC，从而可求出AO，从而求出AF，AC₁，这样即可在Rt△AC₁F中求出cos$∠{C}_{1}AF=\frac{AF}{A{C}_{1}}$，这样即求出了直线AC₁和平面ABCD所成角的余弦值．

解答 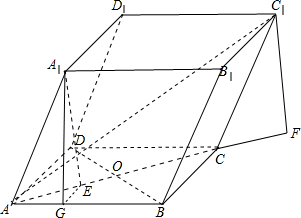解：如图，根据条件知，A₁点在底面ABCD上的射影在∠BAD平分线即AC上，设该射影为E，同样设C₁在底面ABCD上的射影为F，F在AC延长线上；
过E作EG⊥AB，垂足为G，并连接A₁G；
则A₁G⊥AB，A₁G=1•sin60°=$\frac{\sqrt{3}}{2}$，AG=1$•cos60°=\frac{1}{2}$；
又在Rt△AEG中，∠EAG=30°；
∴$GE=AG•tan30°=\frac{\sqrt{3}}{6}$，AE=$\frac{\sqrt{3}}{3}$；
∴在Rt△A₁GE中，${A}_{1}E=\sqrt{{A}_{1}{G}^{2}-G{E}^{2}}=\frac{\sqrt{6}}{3}$；
∴${C}_{1}F=\frac{\sqrt{6}}{3}$，$CF=AE=\frac{\sqrt{3}}{3}$；
连接BD交AC于O，则BD⊥AC，∴$AO=1•cos30°=\frac{\sqrt{3}}{2}$；
∴$AC=\sqrt{3}$，AF=$\frac{4\sqrt{3}}{3}$；
∴在Rt△AC₁F中，$A{C}_{1}=\sqrt{A{F}^{2}+{C}_{1}{F}^{2}}=\sqrt{6}$；
由前面知∠C₁AF是直线AC₁与平面ABCD所成的角；
∴cos∠C₁AF=$\frac{AF}{A{C}_{1}}=\frac{\frac{4\sqrt{3}}{3}}{\sqrt{6}}=\frac{2\sqrt{2}}{3}$．
故选：B．

点评 考查平行六面体的概念，如本题满足∠A₁AD=∠A₁AB时，过A₁作底面的垂线，知道垂足在∠BAD的平分线上，直角三角形边角的关系，知道垂直于同一平面的两直线平行，线面角的概念及求法．