分析 （1）Sn=λan-μ．当n≥2时，Sn-1=λan-1-μ，可得$\frac{{a}_{n}}{{a}_{n-1}}=\frac{λ}{λ-1}$=$1+\frac{1}{λ-1}$为正整数，即可得出正整数λ．
（2）由（1）可得：Sn=2an-μ，可得an=μ•2n-1，因此A={μ（2i-1+2j-1）|1≤i＜j，i，j∈N*}，由于2015∈A，可得2015=μ（2i-1+2j-1）=μ•2i-1（1+2j-i）=5×13×31，利用2i-1为偶数时，上式不成立，因此必有2i-1=1，可得i=1，即可得出j，μ．
（3）当n≥1时，集合Bn={x|3μ•2n-1＜x＜3μ•2n，x∈A}，即3μ•2n-1＜μ（2i-1+2j-1）＜3μ•2n，1≤i＜j，i，j∈N*．Bn中元素个数，等价于满足3×2n＜2i+2j＜3×2n+1的不同解（i，j），只有j=n+2才成立，利用3×2n＜21+2n+2＜22+2n+2＜…＜2n+1+2n+2=3×2n+1，即可得出．（n∈N*）．
解答 （1）证明：∵Sn=λan-μ．当n≥2时，Sn-1=λan-1-μ，
∴an=λan-λan-1，λ≠1，∴$\frac{{a}_{n}}{{a}_{n-1}}=\frac{λ}{λ-1}$，
∴数列{an}为等比数列，
∵各项均为正整数，则公比$\frac{λ}{λ-1}$=$1+\frac{1}{λ-1}$为正整数，λ为正整数，
∴λ=2．
（2）解：由（1）可得：Sn=2an-μ，当n=1时，a1=μ，则an=μ•2n-1，
∴A={μ（2i-1+2j-1）|1≤i＜j，i，j∈N*}，
∵2015∈A，∴2015=μ（2i-1+2j-1）=μ•2i-1（1+2j-i）=5×13×31，
∵j-i＞0，则1+2j-i必为不小于3的奇数，
∵2i-1为偶数时，上式不成立，因此必有2i-1=1，∴i=1，
∴μ（1+2j-1）=5×13×31，
只有j=3，μ=403或j=7，μ=31时，上式才成立，
∴μ=31或403．
（3）解：当n≥1时，集合Bn={x|3μ•2n-1＜x＜3μ•2n，x∈A}，
即3μ•2n-1＜μ（2i-1+2j-1）＜3μ•2n，1≤i＜j，i，j∈N*．Bn中元素个数，
等价于满足3×2n＜2i+2j＜3×2n+1的不同解（i，j），
若j＞n+2，则2i+2j≥2i+2n+3=2i+4×2n+1＞3×2n+1，矛盾．
若j＜n+2，则2i+2j≤2i+2n+1≤2n+2n+1=3×2n，矛盾．
∴j=n+2，又∵（21+2n+2）-3×2n=2+4×2n-3×2n=2+2n＞0，
∴3×2n＜21+2n+2＜22+2n+2＜…＜2n+1+2n+2=3×2n+1，
即i=1，2，…，n时，共有n个不同的解（i，j），即共有n个不同的x∈Bn，
∴bn=n（n∈N*）．
点评 本题考查了等比数列的定义及其通项公式、递推式的应用、分类讨论思想方法，考查了推理能力与计算能力，属于难题．
孟建平小学滚动测试系列答案科目：高中数学 来源： 题型：选择题
| A． | $\frac{{\sqrt{2}}}{3}$ | B． | $\frac{{2\sqrt{2}}}{3}$ | C． | $\frac{{\sqrt{3}}}{3}$ | D． | $\frac{{\sqrt{6}}}{3}$ |
查看答案和解析>>
科目：高中数学 来源： 题型：填空题
查看答案和解析>>
科目：高中数学 来源： 题型：选择题
| A． | $\frac{\sqrt{2}π}{2015}$ | B． | $\frac{2\sqrt{2}π}{2015}$ | C． | $\frac{2π}{2015}$ | D． | $\frac{4π}{2015}$ |
查看答案和解析>>
科目：高中数学 来源： 题型：解答题
查看答案和解析>>
科目：高中数学 来源： 题型：选择题
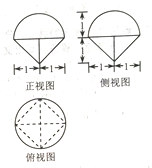
| A． | $\frac{2}{3}（{π+1}）$ | B． | $\frac{4}{3}$（π+1） | C． | $\frac{4}{3}$（π+$\frac{1}{2}$） | D． | $\frac{2}{3}$（π+$\frac{1}{2}$） |
查看答案和解析>>
科目：高中数学 来源： 题型：选择题
| A． | 560 | B． | 880 | C． | 1120 | D． | 1440 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com