
 如图,在边长为1的等边△ABC中D、E分别为AB、AC上的点,点A关于直线DE的对称点A1恰好在线段BC上,
如图,在边长为1的等边△ABC中D、E分别为AB、AC上的点,点A关于直线DE的对称点A1恰好在线段BC上,分析 (1)设∠A1AB=θ∈[0°,60°],用余弦定理表示x与y的关系,利用正弦定理求出AA1,然后用θ表示AD.
(2)通过两角和的正弦函数化简AD的表达式,通过θ的范围求解三角函数的最值.
解答 解:(1)设∠A1AB=θ∈[0°,60°],
则在△A1BA中,由正弦定理得,$\frac{A{A}_{1}}{sin60°}$=$\frac{1}{sin(θ+60°)}$,
∴AA1=$\frac{\sqrt{3}}{2sin(θ+60°)}$
∴AD=$\frac{1}{2}•\frac{A{A}_{1}}{cosθ}$=$\frac{\sqrt{3}}{4sin(θ+60°)cosθ}$ θ∈[0°,60°];
(2)∵4sin(θ+60°)cosθ=2sinθcosθ+2$\sqrt{3}$cos2θ=sin2θ+$\sqrt{3}$(1+cos2θ)=2sin(2θ+60°)+$\sqrt{3}$.
因为θ∈[0°,60°]
所以2θ+60°∈[60°,180°]∴sin(2θ+60°)∈[0,1],
4sin(θ+60°)cosθ∈[$\sqrt{3}$,2+$\sqrt{3}$],∴AD≥$\frac{\sqrt{3}}{2+\sqrt{3}}$=2$\sqrt{3}$-3.
∴AD长度的最小值为2$\sqrt{3}$-3,当且仅当θ=$\frac{π}{12}$时取最小值.
点评 本题考查解三角形的知识,正弦定理的应用,两角和的正弦函数,三角函数的最值的求法,考查计算能力.


 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | |$\overrightarrow{a}$|=|$\overrightarrow{b}$|,$\overrightarrow{a}$=±$\overrightarrow{b}$ | B. | 若$\overrightarrow{a}$∥$\overrightarrow{b}$,则$\overrightarrow{a}$=$\overrightarrow{b}$ | ||
| C. | 若$\overrightarrow{a}$•$\overrightarrow{b}$=$\overrightarrow{b}$•$\overrightarrow{c}$,则$\overrightarrow{a}$=$\overrightarrow{c}$ | D. | 若$\overrightarrow{a}$∥$\overrightarrow{b}$,$\overrightarrow{b}$∥$\overrightarrow{c}$($\overrightarrow{b}$≠0),则$\overrightarrow{a}$∥$\overrightarrow{c}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
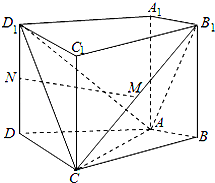 如图,在四棱柱ABCD-A1B1C1D1中,侧棱AA1⊥底面ABCD,AB⊥AC,AB=1,AC=AA1=2,AD=CD=$\sqrt{5}$,且点M和N分别为B1C和DD1的中点.
如图,在四棱柱ABCD-A1B1C1D1中,侧棱AA1⊥底面ABCD,AB⊥AC,AB=1,AC=AA1=2,AD=CD=$\sqrt{5}$,且点M和N分别为B1C和DD1的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com