
已知命题:“若数列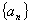 为等差数列,且
为等差数列,且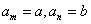
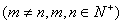 ,则
,则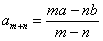 ”.
”.
现已知数列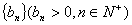 为等比数列,且
为等比数列,且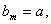
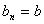
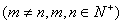 .
.
(1)请给出已知命题的证明;
(2)类比(1)的方法与结论,推导出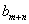 .
.
 同步练习强化拓展系列答案
同步练习强化拓展系列答案科目:高中数学 来源: 题型:
某地区为了解70~80岁老人的日平均睡眠时间(单位:h),随机选择了50位老人进行调查.下表是这50位老人日睡眠时间的频率分布表.
| 序号 (i | 分组 (睡眠时间) | 组中值 (Gi) | 频数 (人数) | 频率 (Fi) |
| 1 | [4,5) | 4.5 | 6 | 0.12 |
| 2 | [5,6) | 5.5 | 10 | 0.20 |
| 3 | [6,7) | 6.5 | 20 | 0.40 |
| 4 | [7,8) | 7.5 | 10 | 0.20 |
|
| [8,9) | 8.5 | 4 | 0.08 |

在上述统计数据的分析中,一部分计算见算法流程图(注:符号“←”与“=”的含义相同),则输出的S的值是________.
查看答案和解析>>
科目:高中数学 来源: 题型:
用反证法证明某命题时,对结论:“自然数a,b,c中恰有一个偶数”正确的反设为( )
A.a,b,c中至少有两个偶数
B.a,b,c中至少有两个偶数或都是奇数
C.a,b,c都是奇数
D.a,b,c都是偶数
查看答案和解析>>
科目:高中数学 来源: 题型:
某地一渔场的水质受到了污染.渔场的工作人员对水质检测后,决定往水中投放一种药剂来净化水质. 已知每投放质量为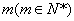 个单位的药剂后,经过x天该药剂在水中释放的浓度y(毫克/升)满足y=mf(x),其中
个单位的药剂后,经过x天该药剂在水中释放的浓度y(毫克/升)满足y=mf(x),其中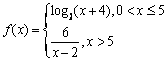 ,当药剂在水中释放的浓度不低于6(毫克/升)时称为有效净化;当药剂在水中释放的浓度不低于6(毫克/升)且不高于18(毫克/升)时称为最佳净化.
,当药剂在水中释放的浓度不低于6(毫克/升)时称为有效净化;当药剂在水中释放的浓度不低于6(毫克/升)且不高于18(毫克/升)时称为最佳净化.
(Ⅰ)如果投放的药剂质量为m=6,试问渔场的水质达到有效净化一共可持续几天?
(Ⅱ)如果投放的药剂质量为m,为了使在8天(从投放药剂算起包括第8天)之内的渔场的水质达到最佳净化,试确定应该投放的药剂质量m的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com