Question

某地一渔场的水质受到了污染．渔场的工作人员对水质检测后，决定往水中投放一种药剂来净化水质. 已知每投放质量为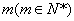个单位的药剂后，经过x天该药剂在水中释放的浓度y（毫克/升）满足y=mf(x)，其中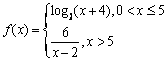，当药剂在水中释放的浓度不低于6（毫克/升）时称为有效净化；当药剂在水中释放的浓度不低于6（毫克/升）且不高于18（毫克/升）时称为最佳净化.

（Ⅰ）如果投放的药剂质量为m=6，试问渔场的水质达到有效净化一共可持续几天?

（Ⅱ）如果投放的药剂质量为m，为了使在8天（从投放药剂算起包括第8天）之内的渔场的水质达到最佳净化，试确定应该投放的药剂质量m的取值范围.

Answer 1

【解析】（Ⅰ）由题设：投放的药剂质量为，

渔场的水质达到有效净化

或 

或，即：，

所以如果投放的药剂质量为，自来水达到有效净化一共可持续8天   .………6分