
【题目】如图,在四棱锥P-ABCD中,PA⊥底面ABCD,底面ABCD为梯形,AD∥BC,CD⊥BC,AD=2,AB=BC=3,PA=4,M为AD的中点,N为PC上一点,且PC=3PN.

(1)求证:MN∥平面PAB;
(2)求二面角PANM的余弦值.
【答案】(1)见解析;(2)![]()
【解析】试题分析:(1)作NH∥BC,根据平几知识可得AMNH为平行四边形,即得MN∥AH. 再根据线面平行判定定理得结论(2)先根据空间直角坐标系,再设立各点坐标,根据方程组解得平面法向量,根据向量数量积求向量夹角,最后根据二面角与向量夹角相等或互补关系得结果.
试题解析: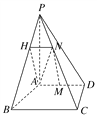
(1)证明:在平面PBC内作NH∥BC交PB于点H,连接AH,
在△PBC中,NH∥BC,且NH=![]() BC=1,AM=
BC=1,AM=![]() AD=1.
AD=1.
∵AD∥BC,∴NH∥AM,且NH=AM,
∴四边形AMNH为平行四边形,∴MN∥AH.
∵AH平面PAB,MN平面PAB,∴MN∥平面PAB.
(2)解:在平面ABCD内作AE∥CD交BC于E,则AE⊥AD.
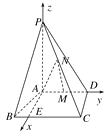
分别以AE,AD,AP所在直线为x轴、y轴、z轴建立空间直角坐标系A-xyz,则P(0,0,4),M(0,1,0),C(2![]() ,2,0),N
,2,0),N![]() .
.
设平面AMN的法向量m=(x,y,z),![]() =(0,1,0),
=(0,1,0),![]() =
=![]() ,
,
则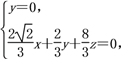 取m=
取m=![]() .
.
设平面PAN的法向量n=(x,y,z),![]() =(0,0,4),
=(0,0,4),![]() =
=![]() ,
,
则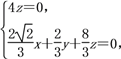 取n=(1,-
取n=(1,-![]() ,0),
,0),
则cos〈m,n〉=![]() =
=![]() ,故二面角PAN
,故二面角PAN![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】对于函数![]() ,若
,若![]() ,则称
,则称![]() 为
为![]() 的“不动点”;若
的“不动点”;若![]() ,则称
,则称![]() 为
为![]() 的“稳定点”.函数
的“稳定点”.函数![]() 的“不动点”和“稳定点”的集合分别记为
的“不动点”和“稳定点”的集合分别记为![]() 和
和![]() ,即
,即![]() ,
,![]() .
.
(![]() )设函数
)设函数![]() ,求集合
,求集合![]() 和
和![]() .
.
(![]() )求证:
)求证:![]() .
.
(![]() )设函数
)设函数![]() ,且
,且![]() ,求证:
,求证:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019年4月23日“世界读书日”来临之际,某校为了了解中学生课外阅读情况,随机抽取了100名学生,并获得了他们一周课外阅读时间(单位:小时)的数据,按阅读时间分组:第一组[0,5), 第二组[5,10),第三组[10,15),第四组[15,20),第五组[20,25],绘制了频率分布直方图如下图所示。已知第三组的频数是第五组频数的3倍。
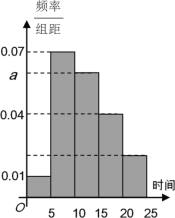
(1)求![]() 的值,并根据频率分布直方图估计该校学生一周课外阅读时间的平均值;
的值,并根据频率分布直方图估计该校学生一周课外阅读时间的平均值;
(2)现从第三、四、五这3组中用分层抽样的方法抽取6人参加校“中华诗词比赛”。经过比赛后,从这6人中随机挑选2人组成该校代表队,求这2人来自不同组别的概率。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() (
(![]() 且
且![]() ).
).
(1)函数![]() 是否过定点?若是求出该定点,若不是,说明理由.
是否过定点?若是求出该定点,若不是,说明理由.
(2)将函数![]() 的图象向下平移
的图象向下平移![]() 个单位,再向左平移
个单位,再向左平移![]() 个单位后得到函数
个单位后得到函数![]() ,设函数
,设函数![]() 的反函数为
的反函数为![]() ,求
,求![]() 的解析式;
的解析式;
(3)在(2)的基础上,若函数![]() 过点
过点![]() ,且设函数
,且设函数![]() 的定义域为
的定义域为![]() ,若在其定义域内,不等式
,若在其定义域内,不等式![]() 恒成立,求
恒成立,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数f(x)的定义域为(0,+∞),且对一切x>0,y>0都有![]() ,当
,当![]() 时,有
时,有![]()
(1)求f(1)的值;
(2)判断f(x)的单调性并加以证明;
(3)若f(4)=2,求f(x)在[1,16]上的值域.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 是定义R的奇函数,当
是定义R的奇函数,当![]() 时,
时,![]() .
.
(1)求函数![]() 的解析式;
的解析式;
(2)画出函数![]() 的简图(不需要作图步骤),并求其单调递增区间
的简图(不需要作图步骤),并求其单调递增区间
(3)当![]() 时,求关于m的不等式
时,求关于m的不等式![]() 的解集.
的解集.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com