
为提高学生的素质,某校决定开设一批选修课程,分别为文学、艺术、竞赛三类,这三类课程所含科目的个数分别占总数的![]() ,现在3名学生独立地从中任选一个科目参加学习。
,现在3名学生独立地从中任选一个科目参加学习。
(1)求他们选择的科目所属类别互不相同的概率;
(2)记![]() 为3人中选择的科目属于文学或竞赛的人数,求
为3人中选择的科目属于文学或竞赛的人数,求![]() 的分布列及数学期望。
的分布列及数学期望。
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案科目:高中数学 来源: 题型:
| 1-1 | 1-2 | 4-1 | |
| 男生 | 75 | a | 40 |
| 女生 | b | 50 | 30 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
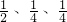 ,现在3名学生独立地从中任选一个科目参加学习.
,现在3名学生独立地从中任选一个科目参加学习.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com