
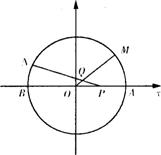
答案:解:以O为坐标原点,AB所在的直线为x轴建立直角坐标系,
则半圆O的方程为x2+y2=4(y≥0),
设∠AOM=2α(0<2α≤π),则∠BPN=α,
∠APN=π-α,点M坐标为(2cos2α,2sin2α),
直线OM的方程为y=xtan2α,
直线PN的方程为y=-(x-a)tanα,
由以上两方程消去α,
可得y[1-![]() ]=
]=![]() ,
,
即1-![]() =
=![]() ,
,
也即(x-a)2-y2=-2x(x-a),
即3(x-![]() a)2-y2=
a)2-y2=![]() ,
,
由此可知点Q在双曲线3(x-![]() a)2-y2=
a)2-y2=![]() 上运动.
上运动.
而该双曲线的渐近线方程为3(x-![]() )2-y2=0,
)2-y2=0,
即y=![]() (x-
(x-![]() a).
a).
设Q(x,y)到两渐近线的距离分别为d1、d2,则3(x-![]() )2-y2=
)2-y2=![]() 总成立.
总成立.
且d1·d2=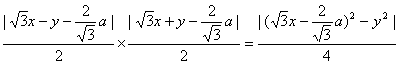
=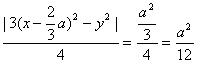 .
.


科目:高中数学 来源: 题型:
 (2012•浦东新区三模)如图,弧AEC是半径为r的半圆,AC为直径,点E为弧AC的中点,点B和点C为线段AD的三等分点,线段ED与弧EC交于点G,且EG=
(2012•浦东新区三模)如图,弧AEC是半径为r的半圆,AC为直径,点E为弧AC的中点,点B和点C为线段AD的三等分点,线段ED与弧EC交于点G,且EG=| 2 | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
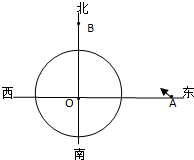 如图,一艘轮船在A处正沿直线返回港口B,接到气象台的台风预报,台风中心O位于轮船正西40km处,受影响的范围是半径为20km的圆形区域.已知港口B位于台风中心正北30km处.
如图,一艘轮船在A处正沿直线返回港口B,接到气象台的台风预报,台风中心O位于轮船正西40km处,受影响的范围是半径为20km的圆形区域.已知港口B位于台风中心正北30km处.查看答案和解析>>
科目:高中数学 来源: 题型:
 (2012•浦东新区三模)如图,弧AEC是半径为r的半圆,AC为直径,点E为弧AC的中点,点B和点C为线段AD的三等分点,线段ED 与弧EC交于点G,且cos∠CBG=
(2012•浦东新区三模)如图,弧AEC是半径为r的半圆,AC为直径,点E为弧AC的中点,点B和点C为线段AD的三等分点,线段ED 与弧EC交于点G,且cos∠CBG=| 4 | 5 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com