
分析 设A(x1,y1),B(x2,y2),线段AB的中点N(x0,y0).直线方程与椭圆方程联立化为:(4k2+1)x2+8kmx+4m2-4=0,利用△>0,化为4k2+1>m2.由于|MA|=|MB|,可得kMN•kAB=-1,利用根与系数的关系、斜率计算公式可得:m(4m-1)(4m2-m-9)<0,解出即可.
解答 解:设A(x1,y1),B(x2,y2),线段AB的中点N(x0,y0).
联立$\left\{\begin{array}{l}{y=kx+m}\\{\frac{{x}^{2}}{4}+{y}^{2}=1}\end{array}\right.$,
化为:(4k2+1)x2+8kmx+4m2-4=0,
△=64k2m2-4(4k2+1)(4m2-4)>0,化为:4k2+1>m2.
∴x1+x2=$\frac{-8km}{4{k}^{2}+1}$,x1x2=$\frac{4{m}^{2}-4}{4{k}^{2}+1}$.
∴x0=$\frac{{x}_{1}+{x}_{2}}{2}$=-$\frac{4km}{4{k}^{2}+1}$,y0=kx0+m=-$\frac{4{k}^{2}m}{4{k}^{2}+1}$+m=$\frac{m}{4{k}^{2}+1}$.
∵|MA|=|MB|,
∴kMN•kAB=-1,
∴$\frac{\frac{m}{4{k}^{2}+1}+1}{\frac{-4km}{4{k}^{2}+1}-0}$•k=-1,
化为:4k2=$\frac{5m+1}{4m-1}$.
∴4k2+1=$\frac{5m+1}{4m-1}$+1>m2,
化为:m(4m-1)(4m2-m-9)<0,由于4m2-m-9>0恒成立,化为m(4m-1)<0.
解得$0<m<\frac{1}{4}$.
∴m的取值范围是$(0,\frac{1}{4})$.
点评 本题考查了椭圆的标准方程及其性质、一元二次方程的根与系数的关系、斜率计算公式、相互垂直的直线斜率之间的关系,考查了推理能力与计算能力,属于难题.


科目:高中数学 来源: 题型:选择题
| A. | 6 | B. | 8 | C. | 12 | D. | 20 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
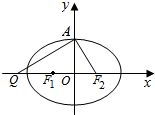 设椭圆C:$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1(a>b>0)的左、右焦点分别为F1,F2,上顶点为A,过点A与AF2垂直的直线交z轴负半轴于点Q,且$2\overrightarrow{{F_1}{F_2}}$+$\overrightarrow{{F_2}Q}$=$\overrightarrow{0}$,若过A,Q,F2三点的圆的半径为2.
设椭圆C:$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1(a>b>0)的左、右焦点分别为F1,F2,上顶点为A,过点A与AF2垂直的直线交z轴负半轴于点Q,且$2\overrightarrow{{F_1}{F_2}}$+$\overrightarrow{{F_2}Q}$=$\overrightarrow{0}$,若过A,Q,F2三点的圆的半径为2.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com