
分析 (Ⅰ)由$α+β=\frac{π}{4}$,借助于两角和的正切化简求值;
(Ⅱ)由已知,把sin2α转化为sin[(α+β)+(α-β)],展开两角和的正弦得答案.
解答 解:(I)∵$α+β=\frac{π}{4}$,
∴tan(α+β)=1.
∴(1+tanα)(1+tanβ)=tanα+tanβ+tanαtanβ+1
=tan(α+β)•(1-tanαtanβ)+tanαtanβ+1
=1-tanαtanβ+tanαtanβ+1=2.
(II)∵$\frac{π}{2}<β<α<\frac{3π}{4}$,∴$π<α+β<\frac{3π}{2}$,$0<α-β<\frac{π}{4}$.
又∵$cos({α-β})=\frac{12}{13}$,$sin({α+β})=-\frac{3}{5}$,
∴$sin(α-β)=\frac{5}{13}$,$cos(α+β)=-\frac{4}{5}$,
∴sin2α=sin[(α+β)+(α-β)]=sin(α+β)cos(α-β)+cos(α+β)$sin(α-β)=-\frac{56}{65}$.
点评 本题考查三角函数的化简求值,考查了“拆角配角”思想的应用,是中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ①② | B. | ②③ | C. | ①④ | D. | ③④ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{9}$ | B. | $\frac{2}{9}$ | C. | $\frac{7}{9}$ | D. | $\frac{8}{9}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
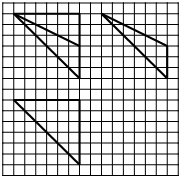 如图,网格纸上正方形小格的边长为1(表示1cm),图中粗线画出的是某零件的三视图,则该零件的表面积为(单位:cm2)( )
如图,网格纸上正方形小格的边长为1(表示1cm),图中粗线画出的是某零件的三视图,则该零件的表面积为(单位:cm2)( )| A. | $27\sqrt{2}+9\sqrt{5}+9$ | B. | $27\sqrt{2}+18\sqrt{5}$ | C. | $9\sqrt{2}+9\sqrt{5}+27$ | D. | $36+9\sqrt{5}+18\sqrt{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com