
分析 (Ⅰ)由ρcosθ=x,ρsinθ=y,能求出线l的直角坐标方程和椭圆C的直角坐标方程.
(Ⅱ)设Q(2cosα,sinα),由点到直线的距离公式能求出|PQ|的最小值.
解答 解:(Ⅰ)∵直线l的极坐标方程为ρcosθ+2ρsinθ+3$\sqrt{2}$=0,
ρcosθ=x,ρsinθ=y,
∴直线l的直角坐标方程为:x+2y+3$\sqrt{2}$=0.
∵椭圆C的极坐标方程为ρ2=$\frac{4}{co{s}^{2}θ+4si{n}^{2}θ}$,
即ρ2cos2θ+4ρ2sin2θ=4,
∴椭圆C的直角坐标方程为x2+4y2=4,即$\frac{{x}^{2}}{4}+{y}^{2}$=1.
(Ⅱ)椭圆C:$\frac{{x}^{2}}{4}+{y}^{2}$=1的参数方程为$\left\{\begin{array}{l}{x=2cosα}\\{y=sinα}\end{array}\right.$(α为参数),
∴设Q(2cosα,sinα),
∴点Q到直线l的距离d=$\frac{|2cosα+2sinα+3\sqrt{2}|}{\sqrt{{1}^{2}+{2}^{2}}}$=$\frac{2\sqrt{2}|sin(α+\frac{π}{4})+\frac{3}{2}|}{\sqrt{5}}$,
∴当$α=2kπ+\frac{5π}{4}$,k∈Z时,d取最小值$\frac{\sqrt{10}}{5}$,
∴|PQ|的最小值为$\frac{\sqrt{10}}{5}$.
点评 本题考查直线、椭圆的直角坐标方程的求法,考查线段长的最小值的求法,考查极坐标方程、直角坐标方程、参数方程的互化,考查点到直线距离公式的应用,考查推理论证能力、运算求解能力,考查转化思想、函数与方程思想,是中档题.


 天天向上口算本系列答案
天天向上口算本系列答案科目:高中数学 来源: 题型:选择题
| A. | ¬p:?x∈(1,+∞),x3+16≤8x | B. | ¬p:?x∈(1,+∞),x3+16<8x | ||
| C. | ¬p:?x0∈(1,+∞),x03+16≤8x0 | D. | ¬p:?x0∈(1,+∞),x03+16<8x0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
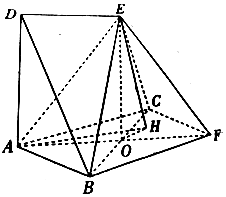 如图,边长为2的正方形ABFC和高为2的直角梯形ADEF所在的平面互相垂直,AF∩BC=O,DE=$\sqrt{2}$,ED∥AF且∠DAF=90°
如图,边长为2的正方形ABFC和高为2的直角梯形ADEF所在的平面互相垂直,AF∩BC=O,DE=$\sqrt{2}$,ED∥AF且∠DAF=90°查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (2,0) | B. | (3,0) | C. | ($\frac{1}{2}$,-1) | D. | ($\frac{1}{3}$,-$\frac{2}{3}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 15 | B. | 9 | C. | 1 | D. | -$\frac{5}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
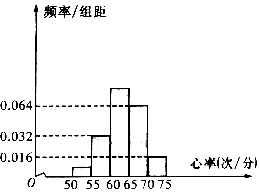 某学校的特长班有50名学生,其中有体育生20人,艺术生30名,在学校组织的一次体检中,该班所有学生进行了心率测试,心率全部介于50次/分到75次/分之间,现将数据分成五组,第一组[50,55),第二组[55,60),…,第五组[70,75),按上述分组方法得到的频率分布直方图如图所示,已知图中从左到右的前三组的频率之比为a:4:10.
某学校的特长班有50名学生,其中有体育生20人,艺术生30名,在学校组织的一次体检中,该班所有学生进行了心率测试,心率全部介于50次/分到75次/分之间,现将数据分成五组,第一组[50,55),第二组[55,60),…,第五组[70,75),按上述分组方法得到的频率分布直方图如图所示,已知图中从左到右的前三组的频率之比为a:4:10.| P(K2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
| 心率小于60次/分 | 心率不小于60次/分 | 合计 | |
| 体育生 | 8 | 12 | 20 |
| 艺术生 | 2 | 28 | 30 |
| 合计 | 10 | 40 | 50 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | $\frac{1}{2}$ | C. | $\frac{π}{6}$ | D. | $\frac{π}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com