
设向量 =(
=( sin x,sin x),
sin x,sin x),  ="(cos" x,sin x),x∈
="(cos" x,sin x),x∈ .
.
(1)若 ,求x的值;
,求x的值;
(2)设函数 ,求
,求 的最大值.
的最大值.
(1) ;(2)
;(2) .
.
解析试题分析:
解题思路:(1)先由两向量的模长相等,求出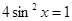 ,再结合
,再结合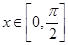 求
求 ;
;
(2)先利用平面向量的数量积定义化简 ,再利用二倍角公式及
,再利用二倍角公式及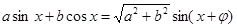 进行化简成
进行化简成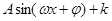 ,再利用角的范围求最值.
,再利用角的范围求最值.
规律总结:1.涉及平面向量的模长、数量积等运算时,要合理选用公式(向量形式或坐标形式);
2.三角恒等变形的关键,要正确运用公式及其变形,如:二倍角公式的变形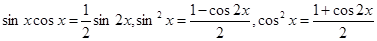 ,
,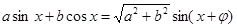
求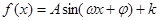 在某区间的值域时,一定要结合正弦函数、余弦函数的图像求解.
在某区间的值域时,一定要结合正弦函数、余弦函数的图像求解.
注意点:学生对公式及其变形运用的灵活性不够,学生应加强公式的记忆和应用;求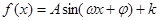 的值域时,学生不善于利用数形结合思想,往往想当然,最大值为1,最小值为-1.
的值域时,学生不善于利用数形结合思想,往往想当然,最大值为1,最小值为-1.
试题解析:(1)由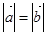 得
得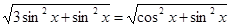 ,即
,即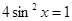 ;
;
又因为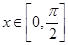 ,所以
,所以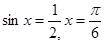 ;
;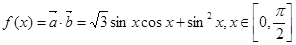 ,
,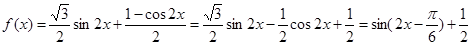 ,
,
又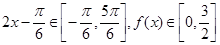 ,即
,即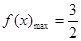 .
.
考点:1.平面向量的数量积、模长公式;2.三角函数恒等变形;3.三角函数的图像与性质.


 中考解读考点精练系列答案
中考解读考点精练系列答案科目:高中数学 来源: 题型:解答题
已知 为坐标原点,
为坐标原点, =(
=( ),
), =(1,
=(1, ),
),  .
.
(1)若 的定义域为[-
的定义域为[- ,
, ],求y=
],求y= 的单调递增区间;
的单调递增区间;
(2)若 的定义域为[
的定义域为[ ,
, ],值域为[2,5],求
],值域为[2,5],求 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知向量a= ,b=(
,b=(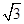 sinx,cos2x),x∈R,设函数f(x)=a·b.
sinx,cos2x),x∈R,设函数f(x)=a·b.
(1)求f(x)的最小正周期.
(2)求f(x)在 上的最大值和最小值.
上的最大值和最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com