
分析 (1)由题意可知:椭圆的标准方程为:$\frac{{y}^{2}}{{a}^{2}}+\frac{{x}^{2}}{{b}^{2}}=1$(a>b>0),c=1,e=$\frac{c}{a}$=$\frac{\sqrt{2}}{2}$,a=$\sqrt{2}$,b2=1,即可求得椭圆E的方程;
(2)由丨PA丨=丨PB丨,利用两点之间的距离公式求得(x1+x2)(k2+1)=-2k(m-$\frac{1}{2}$),①,将直线方程代入椭圆方程,x1+x2=-$\frac{2km}{{k}^{2}+2}$,②,由△>0,m2<k2+2,③代入即可求得实数k的取值范围.
解答 解:(1)由椭圆的焦点在y轴上,设椭圆的标准方程为:$\frac{{y}^{2}}{{a}^{2}}+\frac{{x}^{2}}{{b}^{2}}=1$(a>b>0),
则c=1,e=$\frac{c}{a}$=$\frac{\sqrt{2}}{2}$,a=$\sqrt{2}$,
b2=a2-c2=1,
∴椭圆的标准方程为:$\frac{{y}^{2}}{2}+{x}^{2}=1$;
(2)设A(x1,y1),B(x2,y2),线段AB的垂直平分线过定点P(0,$\frac{1}{2}$),
∴丨PA丨=丨PB丨,即${x}_{1}^{2}+({y}_{1}-\frac{1}{2})^{2}$=${x}_{2}^{2}+({y}_{2}-\frac{1}{2})^{2}$,
∵A,B在l上,则y1=kx1+m,y2=kx2+m,代入求得(x1+x2)(k2+1)=-2k(m-$\frac{1}{2}$),①
则$\left\{\begin{array}{l}{y=kx+m}\\{\frac{{y}^{2}}{2}+{x}^{2}=1}\end{array}\right.$,整理得:(k2+2)x2+2kmx+m2-2=0,
由韦达定理:x1+x2=-$\frac{2km}{{k}^{2}+2}$,②,
由直线和椭圆有两个交点,
∴△>0,即4k2m2-4(k2+2)(m2-2)>0,则m2<k2+2,③
将②代入①得m=$\frac{{k}^{2}}{2}+1$,④,
将④代入③,解得:-$\sqrt{2}$<k<$\sqrt{2}$,
∵k≠0,
∴实数k的取值范围(-$\sqrt{2}$,0)∪($\sqrt{2}$,0).
点评 本题考查椭圆的标准方程,直线与椭圆的位置关系,考查韦达定理,两点之间的距离公式,考查计算能力,属于中档题.


科目:高中数学 来源: 题型:选择题
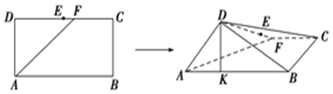 如图,在长方形ABCD中,AB=2,BC=1,E为DC的中点,F为线段EC(端点除外)上一动点,现将△AFD沿AF折起,使平面ABD⊥平面ABCF.在平面ABD内过点D作DK⊥AB,K为垂足,设AK=t,则t的取值范围是( )
如图,在长方形ABCD中,AB=2,BC=1,E为DC的中点,F为线段EC(端点除外)上一动点,现将△AFD沿AF折起,使平面ABD⊥平面ABCF.在平面ABD内过点D作DK⊥AB,K为垂足,设AK=t,则t的取值范围是( )| A. | ($\frac{1}{2}$,2) | B. | ($\frac{1}{2}$,1) | C. | ($\frac{\sqrt{3}}{2}$,2) | D. | ($\frac{\sqrt{3}}{2}$,1) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 165° | B. | 60° | C. | 25° | D. | 15° |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在三棱锥A-BCD中,底面BCD是边长为2的等边三角形,侧棱AB=AD=$\sqrt{2}$,AC=2,O、E、F分别是BD、BC、AC的中点.
如图,在三棱锥A-BCD中,底面BCD是边长为2的等边三角形,侧棱AB=AD=$\sqrt{2}$,AC=2,O、E、F分别是BD、BC、AC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
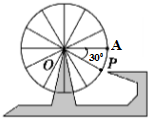 如图所示,一个半径为10m的摩天轮,轮子的底部在地面上2m处,如果此摩天轮按逆时针方向转动,每30s转一圈,且当摩天轮上某人经过点P处(∠POA=30°)时开始计时.
如图所示,一个半径为10m的摩天轮,轮子的底部在地面上2m处,如果此摩天轮按逆时针方向转动,每30s转一圈,且当摩天轮上某人经过点P处(∠POA=30°)时开始计时.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | cosθ<tanθ<sinθ | B. | sinθ<cosθ<tanθ | C. | tanθ<sinθ<cosθ | D. | cosθ<sinθ<tanθ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | (1,3) | B. | (-3,-1)∪(1,3) | C. | (-3,-1) | D. | (0,1) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com