
【题目】已知函数 ![]() .
.
(1)求f(x)的最小正周期和单调递增区间;
(2)如果△ABC的三边a,b,c满足b2=ac,且边b所对角为x,试求x的范围及此时函数f(x)的值域.
【答案】
(1)解:函数 ![]()
= ![]() sin
sin ![]() +
+ ![]() cos
cos ![]() +
+ ![]()
=sin( ![]() +
+ ![]() )+
)+ ![]() ;
;
∴f(x)的最小正周期为 ![]() ,
,
由 ![]() ,
,
解得 ![]() ,
,
∴f(x)的单调递增区间为 ![]() (k∈Z);
(k∈Z);
(2)△ABC中,b2=ac,
∴ ![]() ,即
,即 ![]() ;
;
又x∈(0,π),∴x的取值范围是 ![]() ;
;
由(1)知f(x)在 ![]() 上递增,在
上递增,在 ![]() 上递减;
上递减;
又 ![]() ,
,
∴f(0)<f(x)≤f( ![]() ),
),
即 ![]() <f(x)≤1+
<f(x)≤1+ ![]() ;
;
此时,函数f(x)的值域为 ![]() .
.
【解析】(1)根据三角简单恒等变换,再由正弦函数的图象及其性质得出单调区间,(2)由余弦定理可得出cosx≥![]() ,判断出x的取值范围,结合f(x)的单调区间得出f(x)的值域.
,判断出x的取值范围,结合f(x)的单调区间得出f(x)的值域.
【考点精析】关于本题考查的两角和与差的正弦公式和正弦函数的单调性,需要了解两角和与差的正弦公式:![]() ;正弦函数的单调性:在
;正弦函数的单调性:在![]()
![]() 上是增函数;在
上是增函数;在![]()
![]() 上是减函数才能得出正确答案.
上是减函数才能得出正确答案.


 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案 新思维寒假作业系列答案
新思维寒假作业系列答案科目:高中数学 来源: 题型:
【题目】(本小题满分12分)在△ABC中,角A,B,C的对边分别为a,b,c,C=![]() ,a=5,△ABC的面积为10
,a=5,△ABC的面积为10![]() .
.
(1)求b,c的值;
(2)求cos(B-![]() )的值.
)的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两船驶向一个不能同时停泊两艘船的码头,它们在一天二十四小时内到达该码头的时刻是等可能的.如果甲船停泊时间为1小时,乙船停泊时间为2小时,求它们中的任意一艘都不需要等待码头空出的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲船在岛![]() 的正南方
的正南方![]() 处,
处,![]() 千米,甲船以每小时
千米,甲船以每小时![]() 千米的速度向正北航行,同时乙船自
千米的速度向正北航行,同时乙船自![]() 出发以每小时
出发以每小时![]() 千米的速度向北偏东
千米的速度向北偏东![]() 的方向驶去,当甲,乙两船相距最近时,它们所航行的时间是( )
的方向驶去,当甲,乙两船相距最近时,它们所航行的时间是( )
A. ![]() 分钟 B.
分钟 B. ![]() 分钟 C.
分钟 C. ![]() 分钟 D.
分钟 D. ![]() 分钟
分钟
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数y=loga(x+3)﹣1(a>0,且a≠1)的图象恒过定点A,若点A在直线mx+ny+1=0上,其中m,n均大于0,则 ![]() 的最小值为( )
的最小值为( )
A.2
B.4
C.8
D.16
查看答案和解析>>
科目:高中数学 来源: 题型:
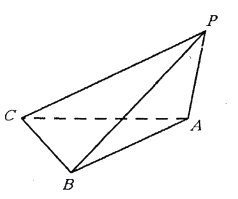
【题目】已知三棱锥 ![]() ,底面
,底面 ![]() 是以
是以 ![]() 为直角顶点的等腰直角三角形,
为直角顶点的等腰直角三角形, ![]() ,
, ![]() ,二面角
,二面角 ![]() 的大小为
的大小为 ![]() .
.
(1)求直线 ![]() 与平面
与平面 ![]() 所成角的大小;
所成角的大小;
(2)求二面角 ![]() 的正切值.
的正切值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校从参加高一年级期中考试的学生中随机抽出60名学生,将其物理成绩(均为整数)分成六段[40,50),[50,60),…,[90,100]后得到如图所示的频率分布直方图,观察图形的信息,回答下列问题:
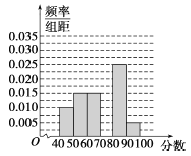
(1)求分数在[70,80)内的频率,并补全这个频率分布直方图;
(2)统计方法中,同一组数据常用该组区间的中点值作为代表,据此估计本次考试中的平均分.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com